【実験計画法】初心者こそ使うべき！次のデータの選び方【D最適基準】 | ゆたろ＠米国生活に怯えるデータサイエンティスト

今回は研究開発分野における機械学習の関連テーマとして、

「どうやって効率的に実験条件を選択してデータを増やすか？」

という悩みを解決してくれる、D最適計画について説明をします。

応用として機械学習での使い方も紹介します。

いわゆるマテリアルズインフォマティクス(MI)ってやつですね！

【超概略】D最適基準による実験計画法とは？
D最適計画とは？
1. 線形モデルとならない場合の対策
【応用】D最適基準を用いた機械学習シミュレーションモデルの作成
D最適基準のデータ範囲
1. ※行列計算の補足
  1. 参考図書

【超概略】D最適基準による実験計画法とは？

直行表といった実験計画法の一つで実験点選択の柔軟性が高いのが特徴
データが偏ることなく実験点を選択できるので機械学習と相性が良い
よく聞くワードとしてベイズ最適化があるが、これとは使い方が異なる
- ベイズ最適化→最適な条件を効率よく見つけ出す
- D最適→データを幅広く集め、傾向を分析したり要因分析を行う

D最適計画とは？

D最適計画とは実験計画法の一つです。

”1回実験をするのに時間やお金がかかってしまう”といったように、コストが高くて繰り返し行うことが難しい場合や”効率的に実験点を選びたい”場合に用いられる手法です。

同じような状況を解決する方法としてはベイズ最適化がありますが、ベイズ最適化は実験条件のベストな設定値を効率的に求めていく方法となります。

まずは、話をイメージしやすくするために最高のペペロンチーノを作る実験をしたいとします。

ペペロンチーノを作ろうとすると恐らく1回の調理で15分から20分くらいかかってしまい、最高の味を研究するにはなかなか試行錯誤が大変です。

そこで登場するのがD最適計画です。

またD最適計画を行うためにはペペロンチーノの味に対して以下の式のように線形モデルの式として表現できることが前提になります。

$$ ペペロンチーノの味y=a_1*(乳化具合)+a_2*(オリーブオイルの量)+a_3*(唐辛子の量)+b $$

つまり、最高のペペロンチーノの材料構成比を予測しようと思ったら係数$a_1,a_2,a_3$の値をそれぞれ調整する必要があります。

係数$a_1,a_2,a_3$を求めるために行列の計算を行います。

$$係数\mathbf{a} = (a_1,a_2,a_3)^T$$

とすると、

$$\mathbf{a}=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}y$$

と表現することができます。

ここで$\mathbf{X}$は以下のように縦に調理実験、横に条件をデータとした表を行列表現したもので、$\mathbf{y}$は各条件で調理した結果の美味しさを表す数値のベクトルです。

実験	乳化具合 (1~5の5段階)	オリーブオイルの量	唐辛子の量
１回目	3	30	5
2回目	2	35	6
3回目	4	50	3

係数$\mathbf{a}$を求めて、美味しいペペロンチーノの線形モデルを構築するためには、

$$(\mathbf{X}^{T}\mathbf{X})^{-1}$$

の逆行列の箇所が解を持っていて計算できる必要があります。

逆に、計算ができなくなるケースは

$$\mathbf{X}^{T}\mathbf{X}$$

が小さい値になる場合です。

そこで、${(}\mathbf{X}^{T}\mathbf{X})^{-1}$が解をもっていて正しく計算できるようにするには、

$\mathbf{X}^{T}\mathbf{X}$の部分が最大となるように$\mathbf{X}$の条件を選んでやるというのが、Ｄ最適基準の考え方になります。

${(}\mathbf{X}^{T}\mathbf{X})^{-1}$の計算ができるようになるには、$\mathbf{X}$が次の条件を満たす必要があります。

類似した条件の候補がない
$\mathbf{X}$(特徴量)の間の相関係数の絶対値が小さい(特徴量同士が類似しない)

線形モデルとならない場合の対策

先ほどのペペロンチーノの例で「俺の作るペペロンチーノの味が簡単な線形モデルで表現できるわけがない」とおっしゃる方、多いと思います。

そういった場合に登場するのが非線形モデルです。

非線形モデルとは説明変数を二乗した項目と交差項を追加した式となります。

つまり、

\begin{split}
ペペロンチーノy&=a_1*(乳化具合)+a_2*(オリーブオイルの量)+a_3*(唐辛子の量)\\
&+a_4*(乳化具合)^2+a_5*(オリーブオイルの量)^2+a_6*(唐辛子の量)^2\\
&+a_7*(乳化具合)*(オリーブオイルの量)\\
&+a_8*(オリーブオイルの量)*(唐辛子の量)\\
&+a_9*(唐辛子の量)*(乳化具合)\\
&+b
\end{split}

として、

線形モデルのときと同様に

$$\mathbf{a} = (a_1,a_2,a_3,a_4,a_5,a_6,a_7,a_8,a_9)^T$$

とすることで、$\mathbf{a}$を前章と同じように計算させることができます。

【応用】D最適基準を用いた機械学習シミュレーションモデルの作成

D最適基準と機械学習予測モデルを利用して、繰り返し実施が必要な工数やコストのかかる実験に対して事前にシミュレーションすることで省力化が見込める小技を紹介します。

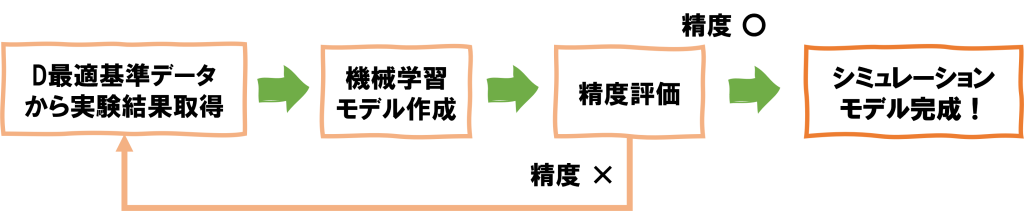
データ取得、モデリングのフロー図

D最適基準を用いたシミュレーションモデルの作成の流れは次の通り。

現実的な範囲内の値を複数取る実験条件$\mathbf{X}$に対して$\mathbf{X}^{T}\mathbf{X}$が大きくなるように$\mathbf{X}$を選定
このとき、データサイズは現実的に実験可能な数値とする。
実験条件$\mathbf{X}$に対する実験結果($\mathbf{y}$)を求める
特徴量(1.で求めた実験条件)と目的変数(2.の結果)からデータセットを作成し、モデル作成を行う
予測させたい新たなデータ(実験条件)$\mathbf{X}_{new}$に対して、3.で作成したモデルを用いて予測を実施
$\mathbf{X}_{new}$に対して、実際に実験を行い、正解データを求める
4.の予測結果と5.の実験結果を比較し、精度が悪いようであれば1．に戻ってデータを追加して再度実施

上記サイクルを回してデータを蓄積し、ある程度精度の良いモデルが完成すればこのモデルを実験前のシミュレーションとして使用することができる。

【ポイント】

- D最適基準によって偏りの少ない(特徴量同士の相関係数の絶対値が小さい)データ生成が可能
- 上記データから機械学習モデルを作成することで、大域的な範囲で精度よく予測(シミュレーション)が可能
- 一度スクリプトを作っちゃえば頭を使わずに実験点を選択することが可能

D最適基準のデータ範囲

D最適基準でデータを取得する場合、気を付けないといけないのが取得するデータの範囲。

ペペロンチーノの例で言うと、

オリーブオイルの量：～最大50g
唐辛子：～最大10g
塩分濃度：1％～5％

というように、料理をするうえで「しょっぱすぎて料理として成り立たない」といったように、条件には限度があるのが普通です。

それ以外にも、

「例えデータが適切な範囲内であったとしても、実際には使えない条件」というケースもあるでしょう。

グラフで表すとこのようなケースです

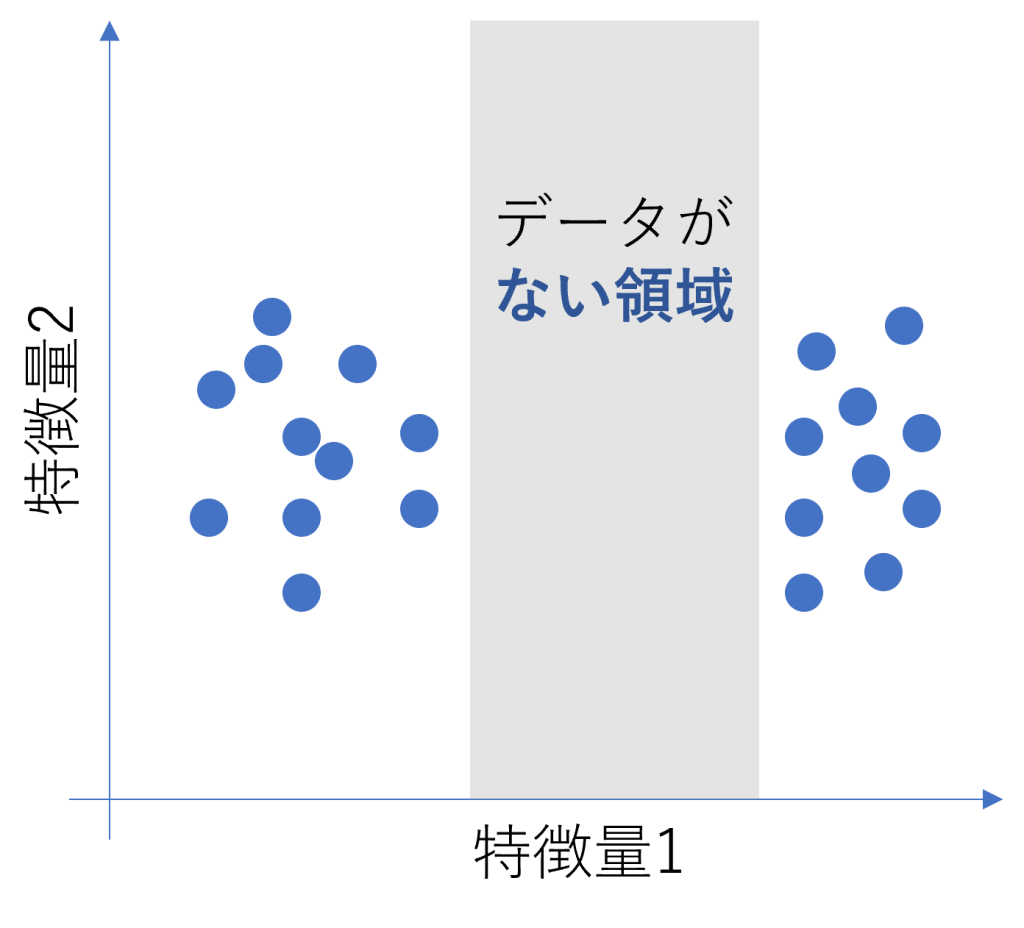
一見、ヒストグラムを見るとデータがあるように見えても、複数の特徴量を考慮すると次のようにデータの無い領域が含まれている可能性もあるので注意が必要です。

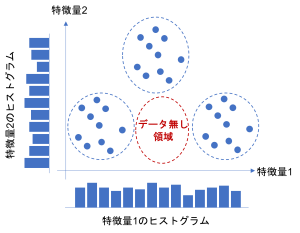
このように、データの偏りというのは一つの特徴量に着目するとわかりやすいですが、複数の特徴量を考慮すると見つけにくい場合があります。

このようなデータで機械学習モデルを作成すると、データの無い領域ではうまく予測することが難しくなります。

※行列計算の補足

（ココより先、数学的な内容に触れます。あまり興味のない人は飛ばしてOK）

ペペロンチーノの線形モデルをn=2にして書き直すと、

$$ Y=b_0+a_1x_1+a_2x_2 $$

$b_0$は切片項とし、YはXから推定される予測値です。

Yは予測値ですので、実際の値とは誤差Fが生じることを考慮すると、

$$ Y=b_0+a_1x_1+a_2x_2+F $$

となり、特徴量の標準化をすることで$b_0=0$とする。

データが$n$行ある場合、

$$Y^{(1)} = a_1x_1^{(1)}+a_2x_2^{(1)}+F^{(1)} $$

$$Y^{(2)} = a_1x_1^{(2)}+a_2x_2^{(2)}+F^{(2)} $$

$$…$$

$$Y^{(n)} = a_1x_1^{(n)}+a_2x_2^{(n)}+F^{(n)} $$

というように表現され、ここで$Y^{(i)},F^{(i)}$はデータのi番目のYの値とFの値。

最小二乗法による線形重回帰分析をしようとすると、この誤差Fは可能な限り小さくしたい→二乗和Gが最小となるように$a_1,a_2$を求める

\begin{split}
F &=Y-b_0-a_1x_1-a_2x_2 \\
G &= \sum^n_{i=1}(F^{(i)})^2 \\
&= \sum^n_{i=1}(Y-a_1x_1^{(i)}-a_2x_2^{(i)})^2 \\
\end{split}

さて、極小値を求める方法と言えば、微分してゼロになる点を見つけることである。

Gに対して$a_1,a_2$で偏微分すると

\begin{split}
\frac{\partial G}{\partial a_1} &= -2\sum^n_{i=1} x_1^{(i)}(Y-a_1x_1^{(i)}-a_2x_2^{(i)})^2=0\\
\frac{\partial G}{\partial a_2} &= -2\sum^n_{i=1} x_1^{(i)}(Y-a_1x_1^{(i)}-a_2x_2^{(i)})^2=0
\end{split}

これを整理して、

\begin{split}
(\sum^n_{i=1} (x_1^{(i)})^{2})a_1 + (\sum^n_{i=1} x_1^{(i)}x_2^{(i)})a_2 &= \sum^n_{i=1}x_1^{(i)}Y^{(i)}\\
(\sum^n_{i=1} x_1^{(i)}x_2^{(i)})a_1+(\sum^n_{i=1} (x_2^{(i)})^{2})a_2 &= \sum^n_{i=1}x_2^{(i)}Y^{(i)}\\
\end{split}

さらに式を分解して行列形式にすると、

\begin{eqnarray}
\begin{pmatrix}
x_1^{(1)} & x_1^{(2)} & … & x_1^{(n)} \\
x_2^{(1)} & x_2^{(2)} & … & x_2^{(n)}
\end{pmatrix}
\begin{pmatrix}
x_1^{(1)} & x_2^{(1)}\\
x_1^{(2)} & x_2^{(2)}\\
…\\
x_1^{(n)} & x_2^{(n)}
\end{pmatrix}
\begin{pmatrix}
a_1\\
a_2
\end{pmatrix}
=
\begin{pmatrix}
x_1^{(1)} & x_1^{(2)} & … & x_1^{(n)} \\
x_2^{(1)} & x_2^{(2)} & … & x_2^{(n)}
\end{pmatrix}
\begin{pmatrix}
Y^{(1)}\\
Y^{(2)}\\
…\\
Y^{(n)}\\
\end{pmatrix}
\end{eqnarray}

となるので、

\begin{eqnarray}
\mathbf{X}=
\begin{pmatrix}
x_1^{(1)} & x_2^{(1)}\\
x_1^{(2)} & x_2^{(2)}\\
…\\
x_1^{(n)} & x_2^{(n)}
\end{pmatrix}
, \mathbf{y} =
\begin{pmatrix}
Y^{(1)}\\
Y^{(2)}\\
…\\
Y^{(n)}\\
\end{pmatrix}
, \mathbf{b} =
\begin{pmatrix}
b_1\\b_2
\end{pmatrix}
\end{eqnarray}

とおくことで最終的には次のように簡素化して表現できる

$$ \mathbf{X}^{T}\mathbf{X}\mathbf{a}=\mathbf{X}^{T}\mathbf{y} $$

ここまでくればもう一息。

上式の正方行列$\mathbf{X}^{T}\mathbf{X}$の逆行列$(\mathbf{X}^{T}\mathbf{X})^{-1}$を両辺に掛け合わせて、

\begin{split}
(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{X}\mathbf{a}&=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y}\\
\mathbf{E}\mathbf{a}&=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y}\\
\mathbf{a}&=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y}\\
\end{split}

※$\mathbf{E}$は単位行列

これまでの流れをまとめると、