今回は機械学習の予測ではなくデータ解析能力を用いて行われる要因分析について説明をしていきます。
要因分析は、「なぜ品質が変わったのか?」や「不良となってしまう原因は何か?」といった要因を分析していく手法です。
特に製造業界においてよく使われます。
機械学習を用いた分析 要因分析
要因分析とは何らかの結果をもたらしている要因(原因)を見つけ出すことです。
売上を例に挙げると、”売上が上がった/下がった理由はなんでやろか?”を突き詰めることです。
- クーポンを発行していた
- セールをしていた
- 天気が良かった
- 経済が良くなった
売上の上下の要因としてはさまざまな理由が考えられますよね。
実際に売上に関する要因分析をする場合、売上を上げる方向にコントロールしたいと思うはずですよね。
つまり、上に挙げた例の中で”天気が良い”とか”経済が良くなった”などは人間の力ではコントロールが難しく、売上の要因分析としての優先度は低くなります。
それでは機械学習を使ってどうやって要因分析をやるのか?という前に疑似相関について説明したいと思います。
要因分析を行うときは疑似相関に要注意!
”相関がある”という言葉の意味は日常生活でも使われると思いますのでイメージはつきやすいですよね。
真夏に気温が高ければ高いほど、ビールの売上が高くなる、みたいな感じです。
では疑似相関とはなんでしょうか。それは、ある二つの事象に対して相関があるように見えてしまい、因果関係があると間違った判断をしてしまうことを言います。
因果関係とは”原因”と”結果”の関係が成り立つことです。
この因果関係をテニスのサーブを例にとってみると、
原因:「スイングスピードが速い」 ⇒ 結果:「ノータッチエースの本数が多い」
原因:「スイングスピードが速い」 ⇒ 結果:「アウトによるミスが多い」
といったように上の二つの例では原因と結果の関係がわかりやすいですね。
次の例ではどうでしょうか。
原因:「ノータッチエースの本数が多い」 結果:「アウトによるミスが多い」
”ノータッチエースの本数”と”アウトによるミスの数”の間には直接的な因果関係はありませんが、次のグラフのようにあたかもこの二つの事象に相関があるように見えます。
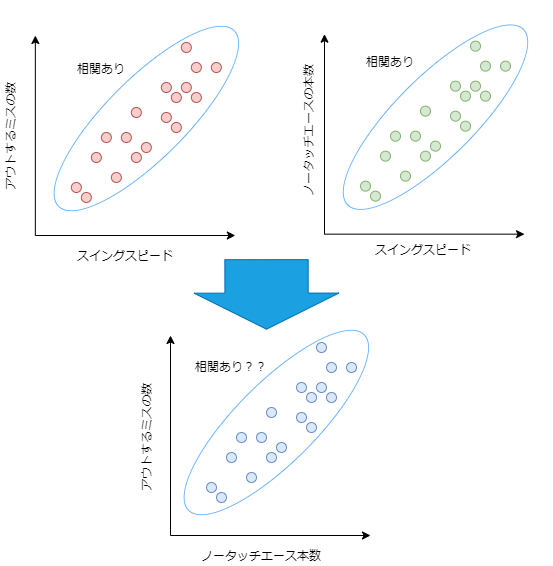
これを擬相関と言います。一見するとこの二つの事象には相関関係があるように見えるため、偽装感が見抜けないと”アウトによるミスの数を増やせばノータッチエースの本数が増える”と間違った解釈をしてしまう可能性があります。
このとき、”スイングスピード”は交絡因子と呼ばれ、本当は影響を与え合う関係ではないのに交絡因子の影響を受けてあたかも関係性があるように見えてしまいます。
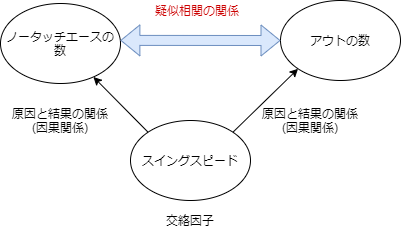
通常、要因分析を行う上で擬相関を見つけたり、交絡因子を探し出すのは非常に手間と時間がかかります。
機械学習を使用する目的が”予測するのみ”であれば、擬相関だろうが精度が上がれば良いのであまり気にする必要はないかもしれませんが、実際のビジネスの現場ではそうもいきません。売上向上の要因分析などは今後施策を有効的に打つために必要な分析となります。
今回のテニスの例でも、ノータッチエースの本数を増やそうと、アウトによるミスの数を増やすトレーニングをしても何の意味もないですからね。
因果関係を明らかにするためには交絡因子の影響を除去しつつ、因果仮説を検証していく必要があり、機械学習モデルから因果関係を導き出せないということに注意が必要です。
機械学習を使った要因分析!要因分析でのモデルインサイト利用
では、本題の機械学習を使った要因分析について説明を行います。
機械学習を使った要因分析の目的は次の通りです。
- 目的変数に対して関係性が強い要因を探索する
- どの説明変数に注目して介入すれば意味のある変化を起こせるかを明らかにする
- 機械学習モデルからは因果関係まではわからない(要注意)
機械学習は目的変数と説明変数の関係性を分析するのが得意なので、この特徴を活かして次のステップで要因分析を行います。
- 要因候補の洗い出し、特徴量エンジニアリング
⇒まずは通常のモデリングを行うための目的変数作成のための準備を行います。 - 要因候補と目的変数との関係性探索
⇒モデリングを行い、精度を評価します。このとき、精度が高ければ高いほど、目的変数と説明変数の関係をうまく分析できていると言えます。 - 要因候補の絞り込み
⇒前回のブログでも紹介したPermutation Importanceを用いて用いて重要な説明変数を絞り込みます。 - 要因候補と目的変数の関係性をモデル化、介入効果の推定
⇒絞り込んだ説明変数を用いて再度モデリングを行い、Partial Dependenceを用いて、重要な説明変数が目的変数に与える影響を評価します。
予測精度が極端に落ちない範囲で以上の1から5のステップを繰り返して説明変数を削減しながらモデリングを行うことで、最終的に重要な要因となり得る説明変数を絞り込んでいくことができます。
また、説明変数を絞り込んでいくもう一つの理由は、多重共線性による影響を低減するためです。
多重共線性は相互に相関する説明変数があった場合、その重要度が過小評価される可能性があります。これは似たような性質のデータが複数あることで、一つ一つの重要度が下がってしまうためです。したがって、似たような性質のデータは片方を削除するなりすることで、より適切に分析を行うことができます。
以上が、機械学習を用いた要因分析です。機械学習によるモデリングを複数回行い、モデリングの過程で得られるインサイト(Permutation ImportanceやPartial Dependence)から目的変数と説明変数の関係性を分析していく手法となります。
む、難しい…!


コメント