【初心者流】Courcera 機械学習 Week 4‐5　を解く！内容：ニューラルネットワーク、バックプロパゲーション

さて、ここからが本番です。今までニューラルネットワークを使った多クラス分類のコスト関数を求めてきました。次に、このコスト関数の最小化問題について考えていきたいと思います。

つまり、$J(\Theta)$を最小とするような$\Theta$を探すことになります。それには

まず、

$$J(\Theta)$$

を計算し、そして

$$\frac{\partial}{\partial\Theta^{(l)}_{ij}}J(\Theta)$$

の計算を行います。

この二つ目の式を計算するために登場するのがバックプロパゲーションと呼ばれる手法です。

バックプロパゲーションの主な目的は、その名前の通り出力側からさかのぼって誤差$\delta^{(l)}_j$を求めていくことです。$\delta$の肩についている文字は$l$番目のレイヤーにあるノード$j$という意味です。

ここでいう誤差とは、実際のラベル$y$とモデルにより出力された予測値との差であり、各ユニットのアクティベーション関数の出力値から期待されるべき値を引いたものです。つまり、誤差$\delta=$予測値‐実際の値　です。

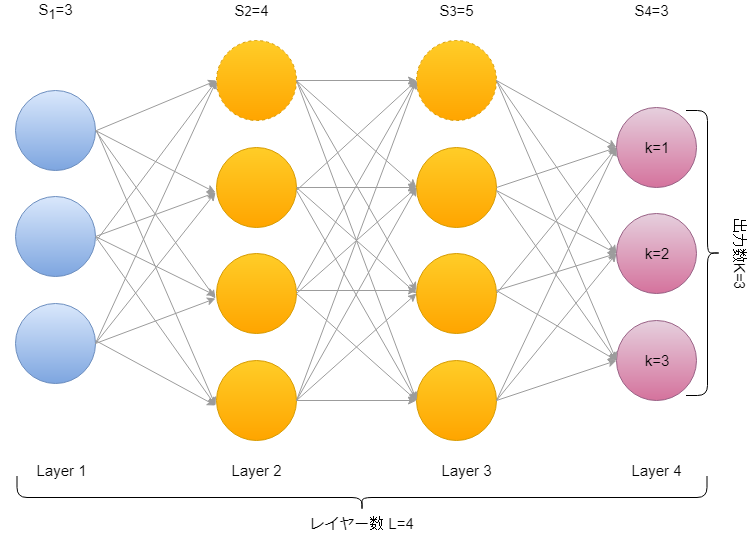
上の図のように、4つのレイヤーを持つ例を考えると、

$\delta^{(4)}_j=a^{(4)}_j-y_j\\$

$\delta^{(3)}=(\Theta^{(3)})^T\delta^{(4)}.*g'(z^{(3)})\\$

$\delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)}.*g'(z^{(2)})\\$

というように$\delta$の項を計算します。ここで、$g'(z^{(l)})$はシグモイド関数$g(z^{(l)})$の一階の微分項であり、$g'(z^{(l)})=g^{(l)}.*(1-g^{(l)})$となります。

$\Delta^{(l)}_{ij}:=\Delta^{(l)}_{ij}+a_j^{(l)}\delta^{(l+1)}_i$

そして計算した誤差$\delta$を足し合わせてアップデートしていきます。

入力層を除く全ての層($l=2,3,…,L$で1層目はトレーニングセットなので実際に観測されている値であるため、誤差とする必要はない)の分だけアップデートしたら、最後に平均化・正規化します。

$D^{(l)}_{ij}:=\frac{1}{m}\Delta^{(l)}_{ij}+\lambda \Theta^{(l)}_{ij}$ if $j \neq 0$

$D^{(l)}_{ij}:=\frac{1}{m}\Delta^{(l)}_{ij}$ if $j = 0$

$\frac{\partial}{\partial\Theta^{(l)}_{ij}}J(\Theta)=D^{(l)}_{ij}$

ということでこれがバックプロパゲーションによるコスト関数の偏微分係数を計算する方法です。

まとめ

・ニューラルネットワークモデルにおけるバックプロパゲーション手法によるコスト関数の偏微分係数の計算を学びました。

ぶっちゃけ、全然わからないっすよね。実際に、CourseraのMachine learningの先生でも直感的に理解できていないかも、と言っています。

実際に実装してみて、使えることが確認できれば深追いしなくてもいいのかもしれませんね。というか、私もですが難しくて理解なんてとてもできない。。。

教授ですら理解が難しいということは、それはもうAIが人類の知能を超えようとしているということなのかもしれませんね。

それでは！