ニューラルネットワークまとめ
今回は、これまでのニューラルネットワーク実装の一連の流れをまとめたいと思います。
少し新しい要素も含んでいますが、その都度説明していきたいと思います。
ニューラルネットワークの手順は以下の通りです。
- \(\Theta\)の初期値をランダムに決定する
- フォーワードプロパゲーションを行い、入力\(x^{(i)}\)に対する\(h_\Theta(x^{(i)})\)を得る
- コスト関数\(J(\Theta)\)を計算する
- バックプロパゲーションを計算し、コスト関数の微分係数\(\frac{\partial}{\partial \Theta^{(l)}_{jk}}J(\Theta)\)を求める
- バックプロパゲーションの実装が正しいか確認する
- 最急降下法やその他の優れた最適解を求めるアルゴリズムを用いてコスト関数\(J(\Theta)\)を最小とする\(\Theta\)を求める
一つずつ見ていきましょう。
1.\(\Theta\)の初期値をランダムに決定する
最初に、\(\Theta\)に初期値を与えてやる必要があるのですが、もし仮に\(\Theta\)をすべてゼロと置いた場合どうなるでしょうか?
\(\Theta\)の値をすべてゼロとしてしまうと、フォーワードプロパゲーションを行う際の各隠れユニットにおいて、アクティベーション関数が\(a^{(2)}_1=a^{(2)}_2\)となり、同じ計算を行っていることになってしまいます。
これを防ぐために、通常は0に近い数値0~1の間でランダムな数値を用います。ちなみにこれをSymmetry breakingと呼びます。かっこいいです。
2.フォーワードプロパゲーションを行い、入力\(x^{(i)}\)に対する\(h_\Theta(x^{(i)})\)を得る
\(\Theta\)の初期値を定めたら、次はフォーワードプロパゲーションの計算を行っていきます。目的は\(h_\Theta(x^{(i)})\)計算することです。
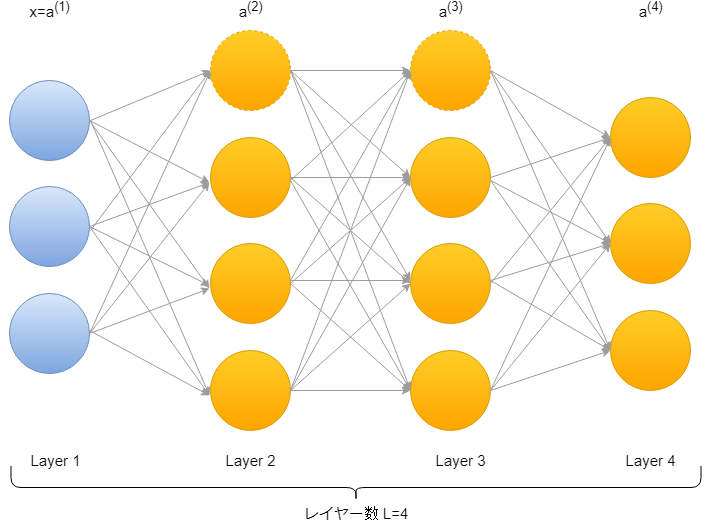
\(a^{(1)}=x\)
\(z^{(2)}=\Theta^{(1)}a^{(1)}\)
\(a^{(2)}=g(z^{(2)})\) (+ \(a^{(2)}_0\))
\(z^{(3)}=\Theta^{(2)}a^{(2)}\)
\(a^{(3)}=g(z^{(3)})\) (+ \(a^{(3)}_0\))
\(z^{(4)}=\Theta^{(3)}a^{(3)}\)
\(a^{(4)}=h_\Theta (x)=g(z^{(4)})\)
と、レイヤー1から順々に計算を行っていきます。
計算方法などの詳細は過去のブログを参照してください。
3.コスト関数\(J(\Theta)\)を計算する
コスト関数を計算していきます。
$$J(\theta)=-\frac{1}{m}[\sum^m_{i=1}\sum^K_{k=1} y^{(i)}_klog( h_\Theta(x^{(i)}))_k+(1-y^{(i)}_k)log(1-(h_\Theta(x^{(i)}))_k)]+\frac{\lambda}{2m}\sum^{L-1}_{l=1}\sum^{s_l}_{i=1}\sum^{s_l+1}_{j=1}(\Theta^{(l)}_{ji})^2$$
大変複雑な式になっております。こちらも過去のブログに詳細を載せています。
→(多クラス分類のコスト関数)
4.バックプロパゲーションの計算
一つ前で計算したコスト関数の微分係数を求めていきます。
\(\frac{\partial}{\partial \Theta^{(l)}_{jk}}J(\Theta)\)
5.バックプロパゲーションが正しいか確認する
自分が計算したバックプロパゲーションが正しいのかどうかを確認する手法があります。それはグラディエントチェッキング(Gradient cheking)と呼ばれています。
\(\frac{\partial}{\partial \Theta^{(l)}_{jk}}J(\Theta)\approx \frac{J(\Theta + \varepsilon)-J(\Theta – \varepsilon)}{2\varepsilon}\)
という関係式からバックプロパゲーションで求めた\(\frac{\partial}{\partial \Theta^{(l)}_{jk}}J(\Theta)\)がなんとなく右辺の計算と合っていることを確かめることができます。
ここで、\(\varepsilon=10^{-4}\)などの小さい値を用いると数学的に微分の計算に近づきます。
つまり、上で示した式はまさに微分の定義に近い形となっており、\(J(\Theta)\)の非常に狭い範囲\(\Theta-\varepsilon\)から\(\Theta+\varepsilon\)(距離は\(2 \varepsilon\))における関数の傾きを計算しているのです。
最初からこっちで計算すればいいじゃん?と思いますが、この計算手法で関数全体を計算してしまうと計算量がとても多くなるため効率的ではありません。なので、あくまで限定された範囲におけるバックプロパゲーションの確認用として使います。
6.コスト関数\(J(\Theta)\)を最小とする\(\Theta\)を求める
さぁ、バックプロパゲーションの計算が問題なさそうということが確認できたらいよいよコスト関数の最小化問題も大詰めです。
これまで、コスト関数を計算し、バックプロパゲーションによるコスト関数の微分係数の計算を行ってきました。あとはこれらを用いて、最急降下法でもそれ以外のL-BFGSといったアルゴリズムを用いて最適化を行い、最終的に\(\Theta\)の値を決定していきます。
最急降下法については過去に説明をしています→最急降下法のやり方
以上がニューラルネットワークを用いた計算方法となります。
長い説明となりましたが、それだけ奥が深いのです。そして、AIなんかに負けないようしっかり理解していきましょう!
- 投稿が見つかりません。


コメント