大規模なデータセットを扱う機械学習
機械学習においてより高いパフォーマンスを得るためには、より良いアルゴリズムを持っていることではなく、より多くのデータを持っていることが重要なのだそうです。
しかしながら、大規模なデータセットを扱うには計算量が増大するという問題がつきまといます。
今日のビッグデータ時代、インターネットトラフィックの情報量を考えると1億個に渡るデータセットを扱う機械学習なんてのも珍しくないのかもしれません。とんでもない計算量ですよね。
さて、ここでは計算量が多くなってしまった場合に効率的に計算できる方法を説明したいと思います。
確率的最急降下法
これまで説明してきた線形回帰やロジスティック回帰モデル、ニューラルネットワークなどのアルゴリズムを作るには、コスト関数の計算が必須となります。大規模なデータセットの場合、このコスト関数を計算するための最急降下法において計算量がネックになってしまいます。
まずは通常のバッチ最急降下法
$$コスト関数J_{train}(\theta)=\frac{1}{2m}\sum^m_{i=1}(h_{\theta} (x^{(i)})-y^{(i)})^2$$
に対して微分項\(\frac{\partial}{\partial \theta_j}J_{train}(\theta)\)の計算を行い、\(j\)個の\(\theta\)について繰り返し更新していくのでした。
$$\theta_j:=\theta-\alpha \frac{1}{m}\sum^m_{i=1}(h_{\theta} (x^{(i)})-y^{(i)})x^{(i)}_j$$
このとき、もしm=3億とか膨大な数であった場合、上記式を\(j\)の数だけ×リピートする回数だけ3億回の足し算を行わなければなりません。
そこで変数を少し改良したのが確率的最急降下法です。
確率的最急降下法のステップとしては
1.データセットをランダムに並べ替える
2.コスト関数の一部を\(cost(\theta,(x^{(i)},y^{(i)}))\)に置き換え、通常の最急降下法同様に微分項を求めましょう。
$$\begin{eqnarray}cost(\theta,(x^{(i)},y^{(i)})) &=& \frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2 \\ J_{train}(\theta) &=& \frac{1}{m}\sum^m_{i=1}cost(\theta,(x^{(i)},y^{(i)})) \\\frac{\partial}{\partial \theta_j}cost(\theta,(x^{(i)},y^{(i)})) &=& (h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}\end{eqnarray}\\$$
3.上記微分項に対して1つのデータを使って計算し、パラメータθの更新を行い、それをデータセット数の数だけm回行います。
\(for \ i=1,2,…,m\)に対して以下の更新を繰り返します。
$$\theta_j:=\theta-\alpha (h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}$$
これにより通常のバッチ最急降下法で行っていた足し合わせの工程を省くことができます。
確率的最急降下法と通常のバッチ最急降下法との違いは、繰り返しθの値を更新していくときの収束の仕方です。
通常のバッチ最急降下法は収束の値まで比較的まっすぐな軌道を描いて収束していきますが、確率的最急降下法では1つのトレーニングデータを計算するため、少しずつ少しずつ遠回りしながら収束へ向かっていきます。また、その収束も求めたい最小の値付近をある一定の小さい範囲でウロチョロし続けますが、実質的にはほとんど問題にならないくらいの値となります。
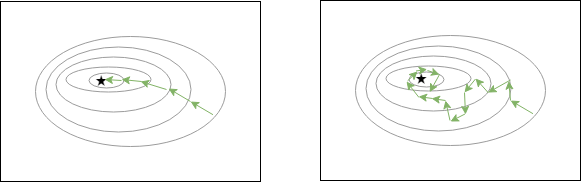
左:通常の最急降下法の収束イメージ
右:確率的最急降下法の収束イメージ
【学習率αについて】
これまで立ててきた確率的最急降下法を用いたモデルが、実際に最小値へと収束しているのかどうかを調べるために、 データセットを最後の1000個だけ用いて\(cost(\theta,(x^{(i)},y^{(i)}))\)をプロットするといった方法があります。
これにより繰り返し回数が多くなるにつれてグラフが収束しているのかどうかを判断することができます。
もし、グラフが発散していってしまった場合は、学習率αを調整しましょう。目安としては、自分で調整するための定数1,2とモデルの繰り返し回数を用いて
$$\alpha=\frac{定数1}{繰り返し回数+定数2}$$
とします。基本的にはαは定数扱いとなります。
※上級者になるとαを変数として繰り返いし回数が増えていくにつれてゆっくりとαを小さくしていくといった使い方をすることもあります。
まとめ
・確率的急降下法によって、大規模なデータセットにも対応できる!
・確率的急降下法の調整は学習率αをいじる!
以上!
次へ:week10 その2 オンライン学習、マップリデュース
- 投稿が見つかりません。


コメント