前回のブログでは作成した機械学習モデルを評価するということで、オーバーフィッティングやアンダーフィッティングの改善方法について説明をしました。
さて、今回は学習曲線(Learning curves)について説明したいと思います。
学習曲線(Learning curvs)
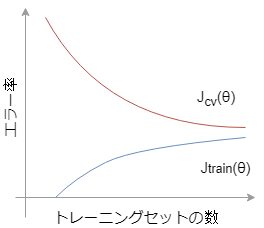
まずは以下のグラフを見てみましょう。横軸に”トレーニングセットの数”、縦軸に”エラー率”を取ったときのコスト関数をプロットしたグラフとなります。
\(J_{train}(\theta)=\frac{1}{2m}\sum^m_{i=1} (h_\theta (x^{(i)})-y^{(i)})^2\)
\(J_{cv}(\theta)=\frac{1}{2m_{cv}}\sum^m_{i=1} (h_\theta (x^{(i)}_{cv})-y^{(i)}_{cv})^2\)
\(J_{train}\)はトレーニングセット数mが少ないとき、例えば\(m=1, 2, 3\)なんて場合、トレーニングセットに対するエラーはゼロに近い値になります。\(m=4, 5, …\)と増えていくと、二次関数でのフィッティングでは誤差が生じてきます。これは、mが増えると全てのトレーニングセットのプロットと一致させる二次関数を探すのが難しくなっていくためです。
従って、トレーニングセットの数mが増えると\(J_{train}\)のトレーニングセットに対するエラー率はより大きくなっていきます。※といってもある一定の値に収束していくことに注意
一方で、クロスバリデーション\(J_{cv}\)はどうでしょうか。
まず、トレーニングセットmが非常に小さいとき、これは\(J_{train}\)が十分に一般化(学習)できておらず、まだ知らないデータセットに対して外れた予測をしてしまいます。学習が足りていない状態です。トレーニングセット数mが大きくなると、エラー率は落ち着いていきます。
従って、\(J_{cv}\)のエラー率を下げるためには、ある程度大きいトレーニング数mで学習する必要があります。
ハイバイアスの場合の学習曲線
あなたのモデルがハイバイアス(アンダーフィッティング)を起こしている場合、\(J_{cv}\)と\(J_{train}\)は以下のようなグラフとなるでしょう。
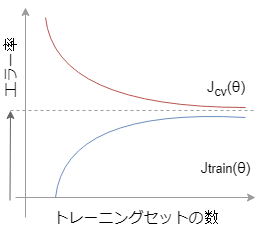
このグラフから見て取れることは、トレーニングセット数を増やしても\(J_{train}\)と\(J_{cv}\)が高いエラー率で落ち着いてしまっています。こうなってしまうと、トレーニングセット数を増やしてもエラー率は大して下がらなくなってしまいます。
つまり、もっと効果的な特徴を持つトレーニングセットを集めたり、多項式を増やしたり、と対策する必要があります。
実際にデータの集め直しとなった場合、大変コストのかかる作業になる可能性があります。現状の予測精度では要件を満たせないのか?データを集めなおすコストはどのくらいか?を考えながら決定していく必要があります。
ハイバリアンスの場合の学習曲線
次にあなたのモデルがハイバリアンス(オーバーフィッティング)を起こしている場合です。
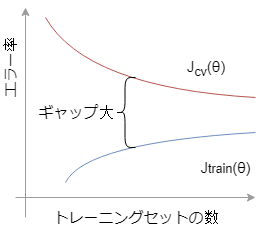
モデルがオーバーフィッティングを起こしている場合、\(J_{train}\)と\(J_{cv}\)のエラー率には大きなギャップがあります。
もしトレーニングセットを増やすことができれば\(J_{train}\)は増加し続け、一方で\(J_{cv}\)は減少し続けてエラー率は落ち着きます。また、正規化の項目を加えることでオーバーフィッティングを改善することも可能です。トレーニングセット数を増やす場合はコストと要相談です。
個人的な意見ですが、世間一般にはオーバーフィッティングは過学習というように説明されていることが多いですが、状況によっては学習が足りなさ過ぎてオーバーフィッティングを起こしていると言えるかもしれません。過学習って言葉ではイメージが合わない気がします。
まとめ
・学習モデルを評価するには学習曲線を見てみることで、オーバーフィッティング気味なのか、アンダーフィッティング気味なのかを判断することができる。
・ハイバイアス(アンダーフィッティング)を改善するには、
‐多項式を増やす(\(x^2_1, x^2_2,x_1,x_2\)など)
‐より効果的な特徴を増やす
‐正規化項のλを減らす
・ハイバリアンス(オーバーフィッティング)を改善するには、
‐トレーニングセット数を増やす
‐特徴数を減らす
‐正規化項のλを増やす
以上、モデルの評価のお話でした!


コメント