ニューラルネットワーク:多クラス分類(One-vs-all)
ニューラルネットワークモデルを用いて多クラス分類を行う例を考えてみたいと思います。十分に学習させたモデルに新しい入力を与えたときに、その入力がなんなのかを判断させるのです。
多クラス分類のニューラルネットワークのイメージはこんな感じです。
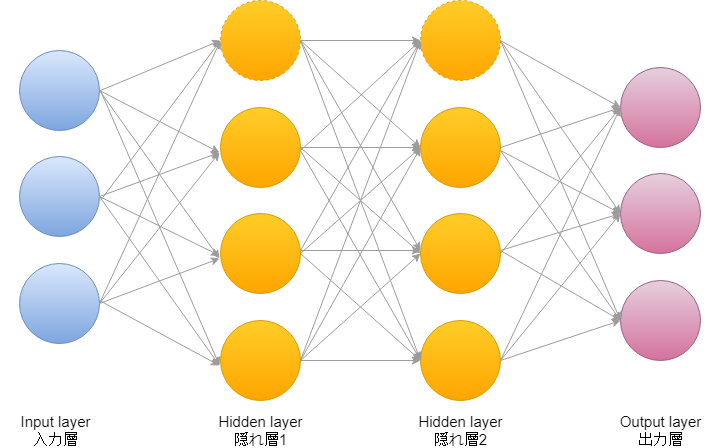
複数の入力に対して、多クラス分類なので出力でノードが複数あります。
例えば、ある画像を入力として使いたいときは画像を構成しているピクセル(画素)を利用します。1ピクセルとは8bitのRGB(赤、緑、青)データですので、ピクセルの位置情報と、このRGBの数値が入力となることになります。
また、教師あり学習を例とするとその入力として使った写真が犬の絵なのか、はたまた水着の女の子の絵なのかというラベルを付け、\(y)\とします。
犬、車、水着の三種類のラベルがあった場合のラベル付けは、実際には次のように行います。
犬の写真 \(=\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\), 車の写真 \(=\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}\), 水着の写真 \(=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\)
つまり\(y=\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\ \), \(\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}\ \), \(\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\ \)というように行列で表現することになります。
上記の要領で写真を何枚も使って学習させたモデルに新しい写真を入力したときに、その写真が何に該当するのかを分類してくれます。
ニューラルネットワーク:多クラス分類のコスト関数
ロジスティック回帰を行うときのコスト関数は、
$$J(\theta)=-\frac{1}{m}[\sum^m_{i=1} y^{(i)}log h_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum^n_{j=1}\theta^2_j$$
これがニューラルネットワークになると
$$J(\theta)=-\frac{1}{m}[\sum^m_{i=1}\sum^K_{k=1} y^{(i)}_klog( h_\Theta(x^{(i)}))_k+(1-y^{(i)}_k)log(1-(h_\Theta(x^{(i)}))_k)]+\frac{\lambda}{2m}\sum^{L-1}_{l=1}\sum^{s_l}_{i=1}\sum^{s_l+1}_{j=1}(\Theta^{(l)}_{ji})^2$$
もう、わからな過ぎて漏らしそうですが詳しく見ていきましょう。
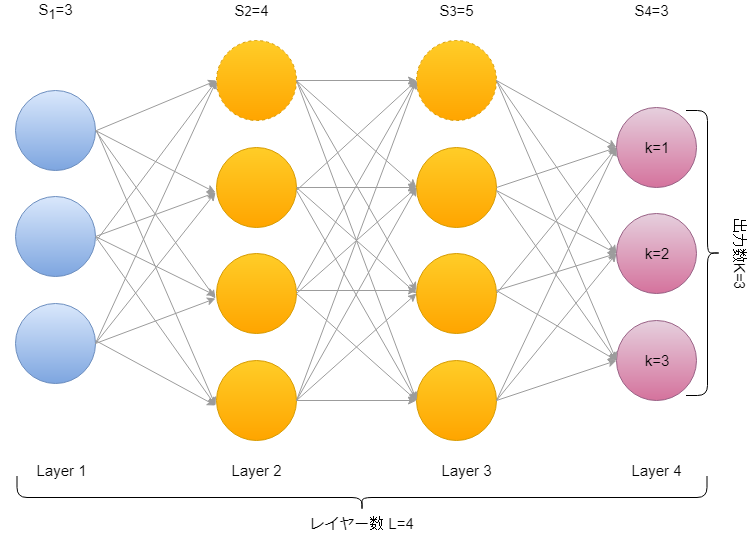
\(L\)はレイヤーの総数で、例えば上の図だと\(L=4\)、そして\(s_l\)は\(l\)番目のネットワークのレイヤーに存在するユニットの数となります。出力層のユニット数は\(K\)で表し、図の場合は\(K=3\)となります。
ニューラルネットワークでのコスト関数は一見、非常に複雑そうに見えますが、やっていることは通常のロジスティック回帰と同じで、それが各層、各ユニットで行われていて、正規化の項が追加されているだけなのです。
次に、バックプロパゲーションという手法を用いて、コスト関数の最小化問題を解いていきます。
- 投稿が見つかりません。


コメント