ロジスティック回帰 多クラスの分類
例えばeメールの分類を行うときに、”仕事関係”、”友達”、”家族”、”趣味”といったように複数のジャンルに分けたいなんてことよくありますよね。
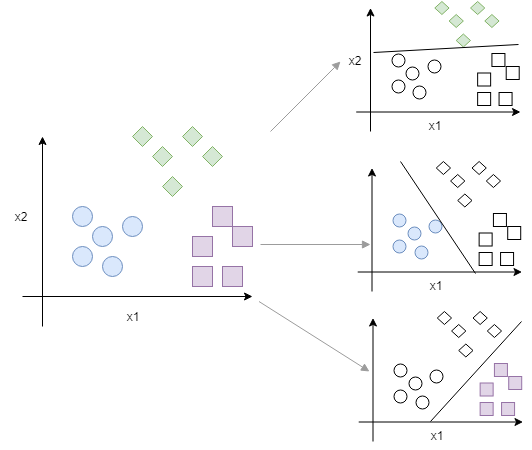
そんなときに使われるOne-vs-allまたはOne-vs-restと呼ばれるロジスティック回帰の手法があります。
クラス分けしたい分類の数が3つの場合は、
$$h_\theta^{(i)}(x)=P(y=i|x;\theta) (i=1, 2, 3)$$
として、それぞれのクラスに対してロジスティック回帰モデル\(h_\theta^{(i)}(x)\)を立てます。つまり、クラス分けしたい数に応じてその数分のモデルができます。
”友達からのメール” か ”それ以外” (Yes/Noの2値)
”家族からのメール” か ”それ以外” (Yes/Noの2値)
”仕事関係のメール” か ”それ以外” (Yes/Noの2値)
といったように2値分類を複数回行っていくイメージです。
各モデル式に対して、シータによって重みづけされた入力\(x\)が与えられたときに\(y=i\)となる条件付確率\(P\)を返す、そんな意味になります。
新しい入力\(x\)が与えられると、\(\max h_\theta^{(i)}(x)\)となるモデル、つまり、\( h_\theta^{(i)}(x)\)が最大となるクラス\(i\)が新しい入力\(x\)の属する予測カテゴリーになります。
カテゴリーの数だけモデルを立てなければならず、少しやっかいです。しかも、条件付確率だなんて聞いたら一気にやる気が減ってしまいそうですが、こらえましょう!
オーバーフィッティング
さて、ロジスティック回帰を行うとよく直面する問題がオーバーフィッティングです。オーバーフィッティングは過学習とも呼ばれ、モデルが学習データに合わせ過ぎてしまったが故に新たなデータに対する予測精度が悪くなる現象です。
次のグラフを見ていきましょう。
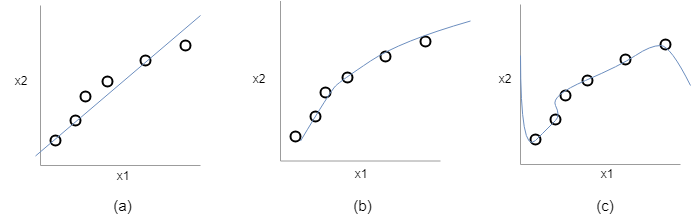
(a):\(\theta_0+\theta_1x\)
(b):\(\theta_0+\theta_1x+\theta_2x^2\)
(c):\(\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+\theta_4x^4\)
まずは(a)のグラフからですが、x1とx2の関係を直線で表現している状況です。(a)の式からもわかります。この状態をハイバイアスまたはアンダーフィッティングと言います。この直線を用いて予測を行ってもある程度の精度は出そうですが、大雑把になっていそうです。
次に、(b)のグラフですが、(a)のグラフより正確にx1とx2の関係を表現しています。式を見てみると\(x^2\)の項が用いられています。多項式を用いてフィットさせるとこのようなカーブを持つグラフとなり、ちょうどよさそうです。
そして最後に(c)ですが、これはオーバーフィッティングまたはハイバリアンス状態と呼びます。これではトレーニングデータに対しては非常に良い予測を行うことができますが、新しいでデータセットに対しては外れた値を予測する可能性があります。
オーバーフィッティングへの対処
このオーバーフィッティングを防ぐには主に二つの方法があります。
・特徴数を減らす
⇒自分で有効そうな特徴を選ぶ(コース後半で変数を圧縮する手法を学びます。)
⇒アルゴリズムモデルを変更する(これについても後半に登場します。)
⇒ただし、精度を落とさないようにどの特徴を選択するかはデータに対して深い知識が必要となり、いくつか特徴変数を変えてモデルを作成し、評価する必要があります。
・正規化
⇒パラメータθの値に対して、正規化項を追加することで値の変動を小さくするという考え方です。
⇒特徴変数の数は変えないので、データに対して知識がなくてもとりあえず実施可能
今回は正規化という考え方を見ていきましょう。
正規化(Regularization)
ここでは、オーバーフィッティングを防ぐために用いられる手法として、正規化を見ていきたいと思います。
$$\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+\theta_4x4$$
一つの例として、仮定関数がポリノミアルな式なっている場合、特徴数が増えて項が増えるとそれだけ\(x^2, x^3,…\)と大きな変数を扱うことになる。そのような多項式はトレーニングセットに対しては非常によくフィットする関数となるが、新たなデータに対してはいまいちな予測をするかもしれない。つまり、オーバーフィッティング状態となります。
これを防ぐために、高次の特徴変数に対応するパラメータθの値を小さくし、目的関数に加えてみよう。
$$J(\theta)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2+1000\theta^3_3+1000\theta^2_4$$
この目的関数を最小化しようとしたときに、\(\theta_3\)と\(\theta_4\)は小さくなくてはならない。つまり、\(\theta_3\)と\(\theta_4\)は今回の例だとほとんどゼロに近い値とし、ほぼ二次関数とすることでオーバーフィッティングを防ぐことができる。
ただし、特徴変数の項目数が多くなった場合は実際にどの特徴が重要でとれを選べばいいのかわからないことも多い。そんなときには全体的にパラーメータを縮めればおkです。
$$J(\theta)=\frac{1}{2m}[\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum^n_{i=i}\theta_j^2]$$
このように二つ目の\(\sum^n_{i=i}\theta_j^2\)の項を追加することで全てのパラメータに寄与することができる。
ところで、この二つ目の\(\sum^n_{i=i}\theta_j^2\)の項は\(i=1, 2,…,n\)となっており、ゼロから始まっていない。通常目的関数を考えるときは\(\theta_0\)から考えることが多いが、機械学習業界の慣例により\(\theta_0\)は正規化されない、らしい。。。慣例ってどうやって決められるのだろうか。。。
そして、λ(ラムダ)は正規化パラメータと呼ばれている。ラムダの目的はトレーニングデータにうまくフィットするようにする、ということと、パラーメータを小さくするという二つの側面を持っています。
ラムダの働きとして、ラムダを大きくすると目的関数の各パラメータθはゼロに近づくため、ラムダの寄与を受けない\(\theta_0\)を切片とする水平直線に近づく。
つまり、ラムダの値が大きすぎるとアンダーフィッティング状態になる。ラムダの選び方には注意が必要!
正規化を用いた最急降下法
さて、正規化を組み込んだ目的関数の最小値問題はどのようにして解くのでしょうか。
タイトル通り以下のようにラムダを追加した最急降下法が使えます。
$$\theta_0:=\theta_0-\alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}$$
$$\theta_j:=\theta_j-\alpha\frac{1}{m}[\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda}{m}\theta_j]$$
上記式にて最小値に収束するまで繰り返し全ての\(j=0, 1, 2,…,n\)に対してシータを更新し続けていきます。
まとめ
- ロジスティック回帰を用いて多クラスへの分類を行いたいときはOne-vs-allまたはOne-vs-rest と呼ばれる手法を用いる。
$$h_\theta^{(i)}(x)=P(y=|x;\theta) (i=1, 2, 3)$$
- ロジスティック回帰モデルを立てる際に、オーバーフィッティングを起こしてしまう場合には正規化を行う。
$$J(\theta)=\frac{1}{2m}[\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum^n_{i=i}\theta_j^2]$$
- 正規化を投入したロジスティック回帰モデルの最小値問題でも、今まで通りの最急降下法が使える。
以上!
- 投稿が見つかりません。


コメント