SVM(Support Vector Machines)
今回から、新しい機械学習アルゴリズムについて説明を行います。
SVM(サポートベクターマシン)ですね。
このSVMは複雑な非線形の関数を学習する方法として知られており、強力で広く使われているアルゴリズムとなります。
SVMはこれまで説明を行ったロジスティック回帰を改良することで得られますので、そのあたりから説明を行っていきます。
まずはコスト関数ですが、シグモイド関数と合わせて以下のような感じでしたよね
コスト関数\(=-(y\log h_\theta(x)+(1-y)\log(1-h_\theta(x)))\)
\(h_\theta (x)=\frac{1}{1+e^{-\theta^T x}}\)
グラフとしては以下のようにり、\(h_\theta (x) \approx 1\)とするには\(\theta^Tx >>0\)、また\(h_\theta (x) \approx 0\)とするには\(\theta^Tx <<0\)とするθを学習する必要がありました。
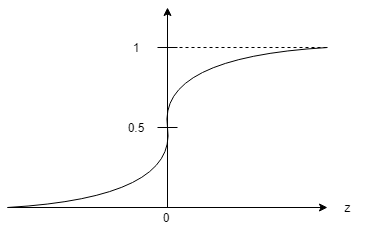
でもこれだと、”もしゼロに近い\(\theta^Tx\)だった場合微妙じゃね?”という疑問が出てきそうですね。
そこで、上記のコスト関数の最小化問題を加味して少し改造して行きましょう。
\(\displaystyle \min_\theta \frac{1}{m} [\sum^m_{i=1}y^{(i)}(\log h_\theta(x^{(i)})+(1-y^{(i)})((-\log(1-h_\theta(x^{(i)})))]+\frac{\lambda}{2m}\sum^n_{j=i}\theta^2_j\)
これを、こうっ!
\(\displaystyle \min_\theta C \sum^m_{i=1}[y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)})]+\frac{1}{2}\sum^n_{j=i}\theta^2_j\)
式中に現れるパラーメタ\(C\)ですが、これはコンベンションと呼ばれ、これまではλにて重みづけを行っていたものが\(C\)に代わります。ちなみに\(\frac{1}{m}\)の項はただの定数であるため、結果的に関与しないのでSVMでは取り除いてしまうのです。
また、
\(-\log h_\theta(x^{(i)})→cost_1(\theta^Tx^{(i)})\)
\(-\log(1-h_\theta(x^{(i)}))→cost_0(\theta^Tx^{(i)})\)
と置き換わっています。
このとき、二つのcost関数は以下のグラフのように、
\(y^{(i)}=1\)のとき\(\theta^Tx{(i)}\geq 1\)であれば\(cost_1=0\)
\(y^{(i)}=0\)のとき\(\theta^Tx{(i)}\leq -1\)であれば\(cost_0=0\)
となるような機能を持たせます。
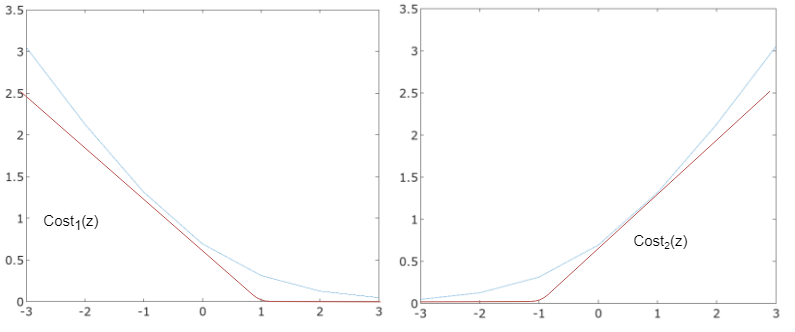
そうすることで、結局は
\(\displaystyle \min_\theta \frac{1}{2}\sum^{n}_{i=1}\theta^2_j\)
となるような\(\theta\)を求める問題に帰結させることになります。
決定境界
サポートベクターマシン(SVM)の分類の仕方はどのように決定境界を定めているのでしょうか。
分類を行った次の二つのグラフを見てみましょう。
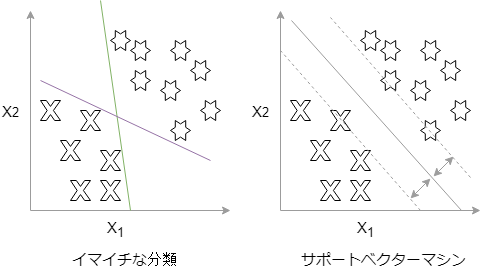
イマイチな分類でも上手くクラス分けができているようですが、緑と紫の二つの線はかなりデータに近いギリギリな分類器になってしまっています。
これでは誤差の多い分類になりかねません。
一方でサポートベクターマシンはというと、まずお互いの分類の境界点に引かれた二つの点線があり、その中心に通る線が決定境界の線となります。
この二つの点線との距離(マージン)が最大になるように黒い線で描いた決定境界が決められます。
このマージンをできるだけ最大にしようとして、分離しようとするのがサポートベクターマシンなのです。
イメージはつかめましたでしょうか。
実際には正規化パラメータ\(C\)の調整が重要な要素となっていきます。データセットの中には外れ値といった極端なデータや誤ったデータが含まれる可能性は大いにあります。
そのようなデータに敏感に反応してしまわないように、うまく無視したりするように、そんな調整をしてやることができます。
また、サポートベクターマシンは線形に分離できないようなデータ(非線形データ)にも対応できます。そこで登場するのがカーネルと呼ばれる手法です。
これらは次回お話します。
以上!
次へ:week7 その2 サポートベクターマシン(カーネル)
- 投稿が見つかりません。


コメント