さて、これまで作ってきた機械学習のモデルですが、もし自身の作成したモデルの予測精度が悪かった場合にはどうすればよいのでしょうか?
・トレーニングサンプルセットを増やす
・特徴を追加する/減らす
・多項式を用いる
・λを増減させる
上記で挙げた様々な方法によって、機械学習モデルを改善することができます。
Coursera 6週目では、どうやってパラメータを調整して良い予測が行われるようになるのか、というところに焦点を当てています。
仮説関数の評価
自分の作成したモデルを評価するために行われる手法として、トレーニングセットを通常のトレーニング用と評価用の二つに分けてやる手法があります。
【トレーニングセット】
\((x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}),…,(x^{(m)},y^{(m)})\)
【テストセット】
\((x^{(1)}_{test},y^{(1)}_{test}), (x^{(2)}_{test},y^{(2)}_{test}),…,(x^{(m)}_{test},y^{(m)}_{test})\)
というように、ラベルも分けてやりましょう。このとき、データをとレーニンセットをテストセットの二つに分ける前に、データをランダムに並べ替える方が良いとされています。
手順としては
1.データをランダムに並べ替え、トレーニングセットとテストセットを7:3の割合で分ける
2.トレーニングセットを用いてコスト関数の最小化問題を解き、\(\theta\)を学習する
3.2.で学習した\(\theta\)及びモデルにテストセットとして残しておいたデータを用いて誤差を計算する(入力xに対して予測値と本当の値との誤差を計算する)
線形回帰モデルであれば、
\(J_{test}(\theta)=\frac{1}{2m_{test}}\sum^{m_{test}}_{i=1}(h_\theta (x^{(i)}_{test})-y^{(i)}_{test})^2\)
ロジスティック回帰モデルであれば、
\(J_{test}(\theta)=-\frac{1}{2m_{test}}\sum^{m_{test}}_{i=1}(y^{(i)}_{test} log h_\theta (x^{(i)}_{test})+(1-y^{(i)}_{test})log h_{\theta}(x^{(i)}_{test})\)
以上の3つのステップにてあなたの作成したモデルが上手くいっているのどうかを判断することが可能となります。
モデル選択問題
次に、あなたが多項式のモデルを考えている場合、いったいいくつの多項式まで追加すればよいのか?とお考えになるかと思います。
そんなときは、まず次のように10個のモデルを作成し、その中からから一つを選びたいとします。
\(d=1, h_\theta (x)=\theta_0+\theta_1x \)
\(d=2, h_\theta (x)=\theta_0+\theta_1x+\theta_2x^2 \)
\(d=3, h_\theta (x)=\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3\)
…
\(d=10, h_\theta (x)=\theta_0+\theta_1x+…+\theta_10x^{10} \)
実際に学習を始める前に今度はデータセットを”トレーニングセット”、”クロスバリデーション”、”テスト”の3つに分けます

【トレーニングセット】
\((x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}),…,(x^{(m)},y^{(m)})\)
【クロスバリデーション(cv)セット】
\((x^{(1)}_{cv},y^{(1)}_{cv}), (x^{(2)}_{cv},y^{(2)}_{cv}),…,(x^{(m)}_{cv},y^{(m)}_{cv})\)
【テストセット】
\((x^{(1)}_{test},y^{(1)}_{test}), (x^{(2)}_{test},y^{(2)}_{test}),…,(x^{(m)}_{test},y^{(m)}_{test})\)
というようにそれぞれの用途に使うラベルも分けてやります。
次のステップとしては、先ほど分けたトレーニングセットを利用してθを学習させます。
\(J_{train}(\theta)=\frac{1}{2m_{train}}\sum^m_{i=1} (h_\theta (x^{(i)})-y^{(i)})^2\)
学習したΘと、クロスバリデーションセットを用いてd=1からd=10までのエラー率を計算します。
\(J_{cv}(\theta)=\frac{1}{2m_{cv}}\sum^{m_{cv}}_{i=1}(h_\theta (x^{(i)}_{cv})-y^{(i)}_{cv})^2\)
そしてモデルが一つに定まったら、そのモデルに対してテストセットを用いてエラー率(一般化エラーと呼びます)を求めていきます。
このようにして、データセットを”Θ学習用”、”モデル選択用”、そして”最終確認用”と3つに分けることであなたのモデルが良い働きをしているのか見極めることができます。
バイアスとバリアンス(アンダーフィットとオーバーフィット)
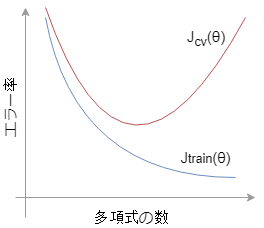
このグラフはトレーニングセットを用いて学習させたモデル\(J_{train} (\theta)\)に、クロスバリエーションセットを突っ込んだ時のエラー率となります。
グラフから、多項式の数が増えるほど\(J_{train} (\theta)\)のエラー率は減少していきます。これは自身のトレーニングセットに対して多項式を増やして良く学習をしているので当然です。
一方、\(J_{cv}(\theta)\)は多項式の数が増えても、ある点を過ぎるとエラー率も上昇してしまいます。
予測を手助けするはずの多項式なのに、エラー率が上昇していくということは、あなたのモデルはオーバーフィッティングを起こしていると言い換えられます。
逆にグラフ左の方向では、自信のトレーニングセットに対してもエラー率が高く、また、多項式の増加によりエラー率が減少していることから、十分にトレーニングがなされておらずアンダーフィッティング状態にあると言えます。
さて、このオーバーフィッティングとアンダーフィッティングはどのように改善すればよいのでしょうか。
まず、挙げられるのは正規化の項を追加することです。
\(J(\theta)=\frac{1}{2m}\sum^{m}_{i=1}(h_\theta (x^{(i)})-y^{(i)})^2+\frac{\lambda}{2m}\sum^m_{j=1}\theta^2_j\)
この式の中の\(\lambda\)を調整してやることでオーバーフィッティング/アンダーフィッティングを改善することができます。
・\(\lambda\)増→オーバーフィット改善
・\(\lambda\)減→アンダーフィット改善
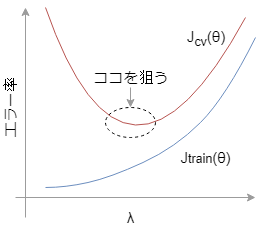
上の図のようにちょうど良いλを選びましょう。
正規化項を追加し、変数λを調整することでオーバーフィッティングやアンダーフィッティングを改善することができます。
ひとまず、ここまで!
- 投稿が見つかりません。


コメント