【初心者流】Courcera 機械学習 Week 2を解く！内容：重回帰分析（多項式）

重回帰分析(多項式を用いる場合)

前回、複数の特徴変数を持つ場合に用いられる重回帰分析について学習しました。

今回は多項式(Polynomial)を用いた仮定関数について説明を行いたいと思います。

次の例を考えてみましょう。

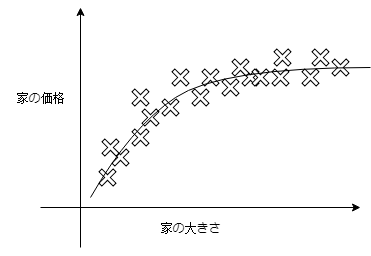
このように、家の大きさに対して家の価格が線形に表現できないことがよくあります。

この場合、もし線形回帰を使って家の価格を予測しようとするとかなり精度の悪い予測となってしまう可能性がありますので、思い切って直線ではなく曲線を使って家の価格を表現したいです。

それを実現するのが多項式です。多項式を用いて仮定関数を以下のようにします。

$$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2$$

後は、実際の目的変数の分布に合わせて特徴変数のルートを取ったり、2乗、3乗の項を追加したり、データに合った曲線を作ることで、予測の精度を上げることが可能です。

実際、この曲線を自動で数式化してくれるツールがあると楽なんですが、よく知りません！（投げやり）

正規方程式(Normal equation)

次に、$\theta$の計算を行うときの目的関数の最小値問題を解決するための手法として正規方程式といういものがありますので簡単に説明したいと思います。

$$\theta=(X^TX)^{-1}X^Ty$$

$$X={x_0, x_1,…, x_n}$$

これを解いちゃいましょう。特徴変数を行列で表現したもの($X$)に対して転置や逆行列といった計算から$\theta$を求めることができます。しかも最急降下法とは違い、学習率αを調整する必要もありません。

が、

正規方程式を解く際には注意が必要です。

それは、特徴変数の項目数が多い場合です。

特徴変数が数百、数千個程度であれば問題はないのですが、数百万個あると逆行列の計算に多大な時間がかかってしまいます。

通常のデータ分析では多くても数千程度ですが、例えば画像認識などを行う場合、画像の画素の情報を特徴変数にする場合など、特徴変数の数に注意が必要です。

まとめ