ロジスティック回帰
機械学習を用いて受信したeメールがスパムメールかそうでないかに分けることを分類(Classification)と呼ぶのでした。
前回の回帰分析は連続値となる数値の予測に用いられてきましたが、スパムメールの判断といったように出力が0か1となるような場合の分類にはロジスティック回帰が用いられます。
さて、このロジスティック回帰を使ってどのように分類を行うのでしょうか?
まずは、回帰分析にも登場した仮定関数を見てみましょう。
$$h_\theta(x)=\theta X=\theta_0x_0+\theta_1x_1+…+\theta_nx_n$$
この式において出力\(h_\theta(x)\)が0または1となってくれると、分類する上では非常に嬉しいのです。
そんなときに用いられる便利な関数がシグモイド関数です。次のような式となります
$$h_\theta(x)=g(\theta X)=\frac{1}{1+e^{-\theta^{Tx}}}$$
ちょっと複雑ですが、仮定関数\(h_\theta(x)\)にまた新たな関数を適応してあげる感じです。
するとこのシグモイド関数は次のようなグラフとなります。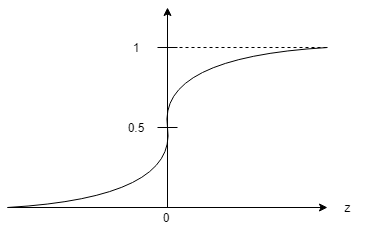
$$z=\theta^{Tx}$$
このシグモイド関数はどのような入力に対しても0か1に近い数値を出力を出してくれます。
なんかこれ、仮定関数の入力に対してその出力の分類(0か1)を行いたいときに使えそうですよね?
”\(h_\theta(x)\geq0.5\)のときに\(y=1\)”、”\(h_\theta(x)<0.5\)のときに\(y=0\) ”
といった感じに分類してやればうまくいきそうです。
このシグモイド関数を用いる他にも、シータのパラメータが決まっていれば決定境界を定めてやり、その境界線より大きかったら1、境界線を下回っていたら0といったように分類する方法もあるようですが、今後はこのシグモイド関数を用いた分類で話を進めたいと思います。
コスト関数、シータの決め方
さて、仮定関数の入力に対して分類を行う方法がわかりました。
が、これで終わりではありません。
ロジスティック回帰においても、回帰分析のときと同じようにシータのパラメータを決定してやる必要があります。
面倒ですね…
しかしながら、基本的な考え方は大きく変わりません。
回帰分析においてコスト関数は次のように求めるのでした。
$$J(\theta)=\frac{1}{2m}\sum^{m}_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2$$
仮定関数\(h_\theta(x^{(i)})\)と実際の分類値である\(y^{(i)}\)の値の差を求めて、その差が小さくなるようにパラメータシータを決めていくのです。
ロジスティック回帰の場合は、出力を0と1に分類したい場合、\(y=0\)か1の2値しか取りません。そんなときに都合の良いlog関数を使います。
$$Cost(h_\theta(x),y)=\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2$$
と、コスト関数から一部を取り出してちょっと表記を変えてあげます。そして、この取り出した部分(\(Cost(h_\theta(x),y)\))にlog関数を用いて、
\(y=1\)のとき\(Cost(h_\theta(x),y)=-\log(h_\theta(x))\)
\(y=0\)のときに\(Cost(h_\theta(x),y)=-\log(1-h_\theta(x))\)
としてやります。ぶっちゃけ高校生のときからわかりにくいlog関数ですが、グラフにするとなんとなくイメージできます。
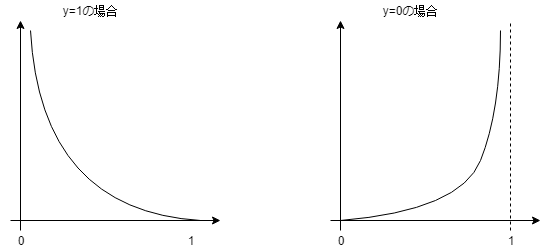
左のグラフ:\(-\log(h_\theta(x))\)、右のグラフ:\(-\log(1-h_\theta(x))\)
実際の出力\(y=1\)に対して、仮定関数\(h_\theta(x)=1\)となればコスト0となり、\(h_\theta(x)=0\)となるとコストが無限大に近づいてしまいます。
同様に、
実際の出力\(y=0\)に対して、仮定関数\(h_\theta(x)=0\)となればコスト0となり、\(h_\theta(x)=1\)となってしまうとコストが無限大に近づいてしまいます。
少しはlog関数のイメージができましたね(多分)
そしてこの式は一つにまとめることができます。
$$J(\theta)=\frac{1}{m}\sum^{m}_{i=1}Cost(h_\theta(x),y)\\=\frac{1}{m}[\sum^{m}_{i=1}y^{(i)}\log (h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]$$
このようにy=0の場合とy=1の場合ではどちらかが必ずゼロとなるので足し合わせて表記することができます。場合分けを行う必要もなくなるのです。
さて、コスト関数が出来上がりましたので、後はシータを決めていきましょう!いつもの最急降下法を用いて。
そう、コスト関数\(J(\theta)\)を最小とするようなシータを求めるために、
$$\theta_j:=\theta_j-\alpha\frac{1}{m}\sum^{m}_{i=1}(h_\theta(x^{(i)})-y^{(i)})$$
の処理を\(j=0, 1,…,n\)それぞれについて繰り返し行います。
これは回帰分析の時と全く同じです。学習率αの決め方には注意しましょう。
まとめ
・ロジスティック回帰は分類を行うときに用いる。
・これまでの回帰分析でで用いた目的関数にシグモイド関数を適用すればよい。
- 投稿が見つかりません。


コメント