前回に引き続き、Courcera機械学習の解説を偉そうにやっていきたいと思います。
数式らしい数式も出てきますので、心してかかっていきましょう。
さて、前回のおさらいですが、データからある数値を予測したい場合は何を用いるんでしたっけ?
そう、回帰解析ですね。
今回はこの回帰解析についてさらに詳しく説明していきます。
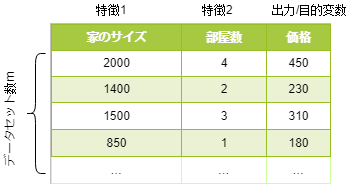
これから出てくる単語:トレーニングセット
機械学習アルゴリズムに学習させるためのデータです。説明変数とその目的変数のセットとなります。そのセット数を”m”という変数で表すのが一般的なようです。
また、下表の”家のサイズ”と”部屋数”といったように入力xが複数あります。これらを特徴変数(フィーチャー)と呼びます。
つまり、機械学習においては”特徴変数(家に関する情報)を用いて目的変数(家の価格)をどう表現できるか”を計算していきます。
トレーニングセット表
単一変数の線形回帰モデル
単一変数回帰解析モデルを使って任意の入力に対する出力を予測するためには以下のような流れになります。
- トレーニングセットを使って学習アルゴリズムを学習させ、仮定関数ℎを作る
- 任意の入力を仮定関数ℎにぶち込み、予測値を出力する
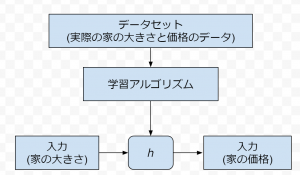
単一変数回帰解析モデルの流れ
以上より、機械学習を用いて回帰解析を行うためにまずは、仮定関数ℎを作ってやる必要があります。
それでは仮定関数ℎはどのようなものでしょうか。次の数式を見てください。
$$h_\theta(x)=\theta_0+\theta_1x$$
$$仮定関数h_\theta(x)は入力xと\theta_0や\theta_1によって決められる。\\$$
この式の意味を直感的に理解する次のグラフをご覧ください。
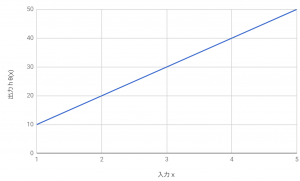
$$h_\theta(x)=\theta_0+\theta_1x$$
$$\theta_0は切片のパラメータ、\theta_1は傾きのパラメータであることがわかります。$$
このように、パラメータθをうまいこと決めてやることで、入力(家の広さ)に対する出力(家の価格)を予測することができます。
つまり、学習アルゴリズムと任意の入力を用いて出力数値を予測するには、トレーニングデータを用いてパラメータθを上手いこと決めてやることが必要になります。
それではどうやってパラメータθを決めていくのでしょうか?
コスト関数 パラメータθの決定
さて、先ほど登場した仮定関数は、
$$h_\theta(x)=\theta_0+\theta_1x$$
と書くのでした。
このパラメータθを決めるためには、こうします。
コスト関数:
$$J(\theta_0, \theta_1)=\frac{1}{2m}\sum^{m}_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2$$
ターゲット:
$$\min J(\theta_0, \theta_1)となるような\theta_0, \theta_1を探す$$
つまり、コスト関数Jを最小とするようなθを探せば良いのですが、その前にこのコスト関数は何を表しているのでしょうか?
それは、
$$”実際のyの値とh_\theta(x)との差”$$
を表しています。
つまり、コスト関数Jは仮定関数による予測値とトレーニングセットの目的変数との差を表しているので、この差が小さくなるようにθを調整してやればいいのです。※下図参照
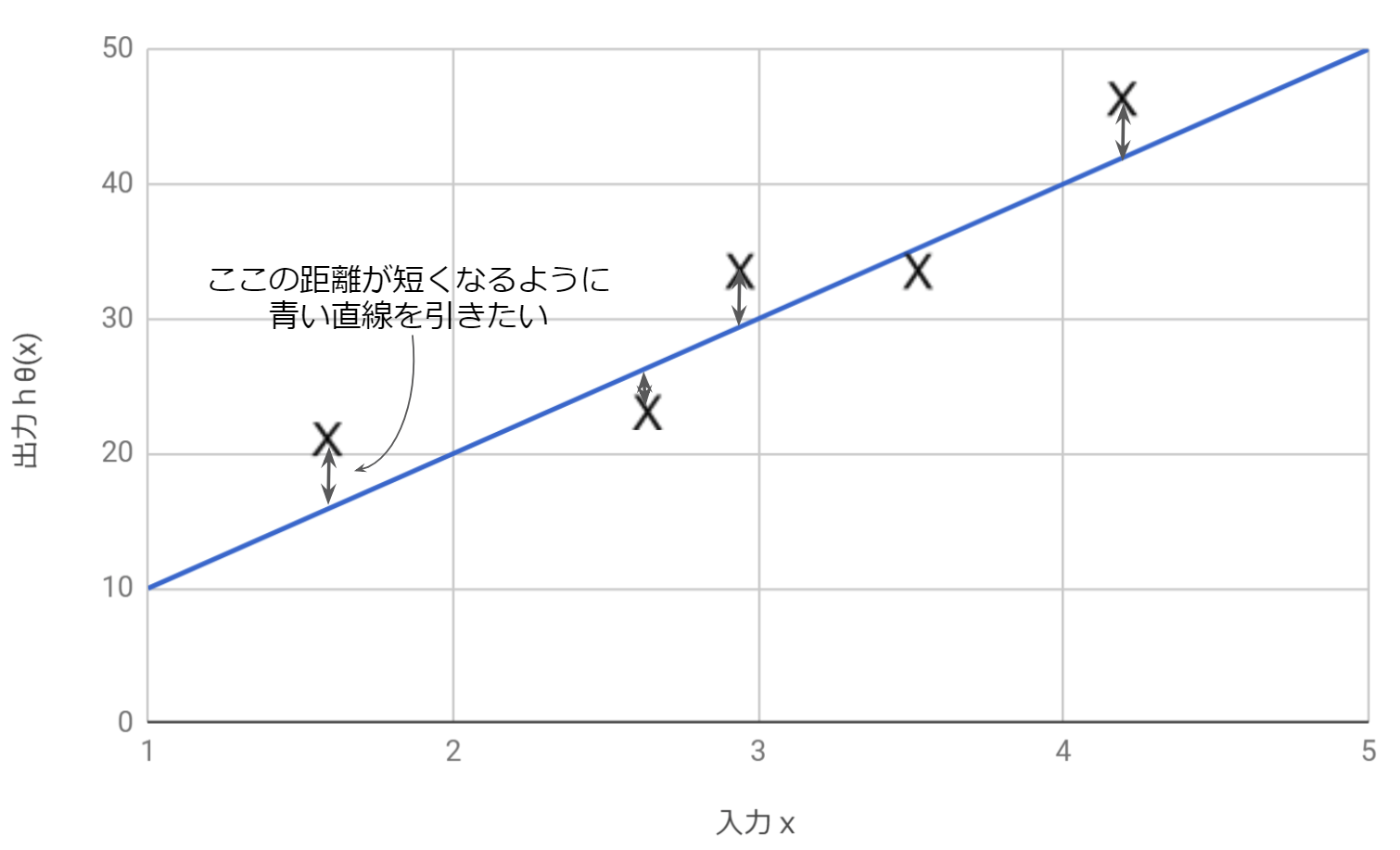
コスト関数Jと実際の出力
さて、コスト関数がどういう意味を持つのか理解できたでしょうか。
次はこのコスト関数を最小とするθをどうやって探すのか、見ていきましょう。
最急降下法
学習アルゴリズムをトレーニングさせるためにはコスト関数Jが最小となるようにθを定めてやる必要があるとわかりました。
$$J(\theta_0, \theta_1)$$
$$\min_{\theta_0, \theta_1}J(\theta_0, \theta_1)$$
これを実現するには最急降下法と呼ばれる最小値を求めるための少し小難しいテクニックが必要となります。
手順はこんな感じです。
1.\(\theta_0\)と\(\theta_1\)を初期化する\((\theta_0=0, \theta_1=0)\)
2.初期化したスタート地点から\(J(\theta_0, \theta_1)\)が最小値に向かうように\((\theta_0, \theta_1)\)を更新していく
簡単に言うと、コスト関数J上にあるスタート地点(初期化した値)からコスト関数Jが減少していき、最小値に向かっていくようにθを更新していく、ということ。
ここでポイントとなるのは2.の”最小値に向かうように”というところですが、これはどのようにして実現するのでしょうか。
最小値に向かうというのは言い方を換えると、”グラフの傾きが小さくなり、ゼロとなるように”ということです。
グラフの傾きを求めるときに皆さんなんとなく覚えている人も多いと思いますが、その通り。
偏微分の登場です。微分ではなく、偏微分です。
偏微分は関数の中に複数の変数がある場合、その変数を指定して微分を行うといった感じだと私は理解しているのですが、詳しい説明は数学の教科書を参照してください!
それでは、偏微分を用いてθをそれぞれ更新していきましょう。
$$\theta_0:=\theta_0-\alpha\frac{\partial}{\partial \theta_0}J(\theta_0, \theta_1)$$
$$\theta_1:=\theta_1-\alpha\frac{\partial}{\partial \theta_1}J(\theta_0, \theta_1)$$
あぁ、過去の学生時代の悪夢が蘇ってきたかのような素晴らしい数式ですね。
この二つの式かが意味するところは、
1.コスト関数Jの偏微分にα(学習率と呼んでいます)という定数を掛け合わせる
2.更新前のθから1.の結果を引いたものを新たなθとして更新する
ということです。
つまり、コスト関数を偏微分してθの値を更新し続けたときに、グラフの傾きがゼロに限りなく近くなる(収束する)位置をグラフの極小値(最小値)であるという捉え方をします。
学習率α
学習率αについてはαの値が大きければθは大きく大胆に更新されますが、目的の最小値を飛び超えてしまい、なかなか収束しない可能性があります。逆に小さ過ぎると最小値にたどり着くまでに何度も更新しなければならず、計算量が増えてしまいます。
下の図は、学習率αを変えてた時にどのように最小値に向かうのかをイメージしたものです。
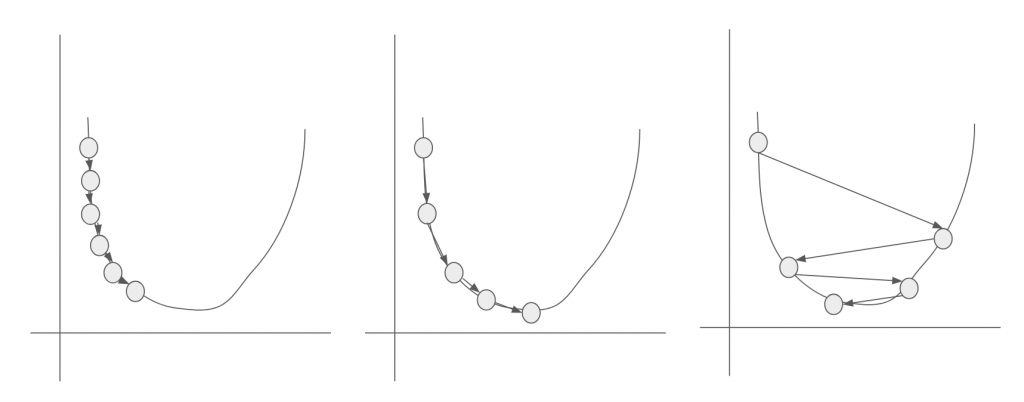
左側:αが小さい値 中心:αが適正値 右側:αが大きい値
まとめ
以上で、コスト関数Jが最小となるθの値を求めることができました。
さて、θが求まったら次はいよいよ仮定関数を使ってさっそく予測を行いたい!
ところですが、特徴変数が一つでは予測するにも寂しいものですので、複数の特徴変数を用いた場合の処理について説明を行いたいと思います!
それではお元気で!
- 投稿が見つかりません。


コメント