【初心者流】Courcera 機械学習 Week 8を解く！内容：次元削減

主成分分析(PCA:Principal Components Analysis)

機械学習を行う上で、サンプルデータ量がとてつもなく膨大な数になってしまい、計算量などの負荷が非常に大きくなることがしばしあると思います。

そんなときはデータ量を圧縮することでメモリやディスク容量を節約したり、学習アルゴリズムのスピードアップにつなげることができます。

データ圧縮の手法としてよく用いられるのが主成分分析(PCA)です。PCAはもともと\(n\)個の特徴を持つ\(n\)次元のサンプルデータに対して、それらのデータの射影誤差を最小とするk個の方向ベクトル(\(u^{(1)},u^{(2)},…u^{(k)}\))を見つけ出すことで、\(n\)次元から\(k\)次元のデータへと変換します。

また、射影誤差とは以下のグラフのように2次元のデータをある直線上に射影させる際に各データと直線との距離を意味し、PCAはこの射影誤差が最小となるような直線(各データからの垂線と直行する直線)を選択します。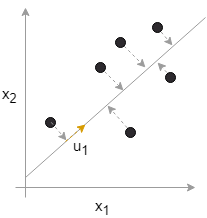ちなみにPCAを用いて3次元のデータ(\(x^{(1)},x^{(2)},x^{(3)}\))を2次元に圧縮する場合は、直線ではなく二次元平面上(\(u^{(1)},u^{(2)}\))に射影されます。4次元以上になってしまうとグラフによる可視化が難しくなってしまいます。

この、誤差を最小とするような直線なり平面なりを求める作業は線形回帰直線に似ていますが、アルゴリズムは異なります。線形回帰の目的はyを予測することですが、PCAでは予測したいyの値はありません。

それではPCAはどのようにして方向ベクトルを見つけていくのでしょうか。そのステップを説明したいと思います。

１．データのスケーリング、正規化

まずはスケーリングや正規化を行い、各特徴の数値のレンジを合わせます。これは例えば\(x^{(1)}\)が”家の値段”、\(x^{(2)}\)が”部屋の数”だった場合、数値だけをみてしまうと家の値段の方がとんでもなく大きい値になってしまいますよね？こういったことを防ぐためにスケーリング、正規化を行います。

スケーリングについは過去の記事でも書いていますのでそちらも参照ください。

まずは平均を求めて正規化

$$\mu_j=\frac{1}{m}\sum^m_{(i=1)}x^{(i)}_j$$

$$x^{(i)}_j=\frac{x^{(i)}_j-\mu_j}{データの標準偏差S_j}$$

二つ目の式の分母は、今回用いた標準偏差のほかに”(最大値)-(最小値)”なども使うことができる。

2．共分散行列の計算

共分散行列:

$$\Sigma=\frac{1}{m}\sum^n_{(i=1)}(x^{(i)})(x^{(i)})^T$$

OctaveやMATLABで計算するときはこんな感じです

$$Sigma=(1/m)*X’*X;$$

3．共分散行列の固有値の計算

svd()はカッコ内の行列に対して特異値の計算を行うOctaveやMATLABのライブラリの一つです。

計算によって出てきた答えから実際に使うのは[U, S, V]のうちUのみで、これが共分散行列の固有値の計算結果となります。

\begin{eqnarray}U=\left( \begin{array}{ccc} | & | & & | \\ u^{(1)} & u^{(2)} & … & u^{(n)} \\ | & | & & | \end{array}\right)\end{eqnarray}

\(x^{(i)}\)は\(n\)×1行列であり、その転置である\((x^{(i)})^T\)は1×\(n\)行列となるので、Uはn×n行列となります。

4．低次元なベクトルzを見つける

先ほど求めた共分散行列の固有値Uの最初のk列までを取り出してUとして、データセット\(x\)と掛け合わせます。

$$z=U^T*x$$

このとき、共分散行列の固有値から取り出したk列のkの値によって次元数を変えることができますが、このkの選び方は注意が必要です。

kの値を小さくするといことは、もともと持っていた情報量を削るということですので、むやみに小さくしていいものではありません。

そこで、もともとのデータ平均と射影誤差の平均の比を取り、どれだけ元の情報を保持しているかを表現することができます。

$$\frac{\sum^m_{(i=1)}||x^{(i)}-x^{(i)}_{approx} ||^2}{\sum^m_{(i=1)}||x^{(i)}||^2}\leq 0.01$$

この計算の結果、例えば0.01以下となるようにしてやると、PCAによる圧縮結果でも99％以上の分散が保持されているという解釈になります。

また、固有値の計算から求めた[U, S, V]のうちSはｎ×ｎの正方行列であり、対角行列でもあります。そして以下のようにあるkの値を確認したい場合に、

$$\frac{\sum^k_{i=1}S_{ii}}{\sum^m_{i=1}S_{ii}}\geq0.99$$

を計算します。

これはサンプルデータ数mつまり対角成分全ての和を分母にして、分子に1からkまでの対角行列の和を取ります。

kの値を変えていき、上式が99％となるkの値を探し出すことで元のデータの分散の99％が保持されるkの値を得ることができます。

以上が、PCAによる次元削減の方法です。

まとめ

・PCAを用いてn次元のサンプルデータに対して任意のk次元までデータを圧縮することが可能！

・ただし、kを小さくしてしまうと元々持つ情報量が分散してしまうため、99％以上保持できるkを探す

あなたの機械学習アルゴリズムを強化させるためのツールとしてPCAはとても有能そうですね！以上です。

次へ：week9 アノマリー検知(異常検知)

• 投稿が見つかりません。