今回からいよいよニューラルネットワークに入っていきたいと思います。名前からしてなんとなく最先端な感じがしますね!
そもそもニューラルネットワークは極めて古いアルゴリズムであり、脳を模倣することを目的としている。つまり、人間の脳が行っている処理、つまり目で見たものが何なのか理解したり、食べた物が何なのか理解したりする機能をアルゴリズム的に模倣してやれば人間ができるような分類が機械にもできるんじゃないか、という背景があるようです。
しかしながら、この脳を模倣したニューラルネットワークは計算量がとても多く、近年のコンピュータの発達によってなってようやく大規模なニューラルネットワークを走らせられるようになった、というわけです。
というようなニューラルネットワークについてのウンチクを知りたい人はCourceraへGO! (https://www.coursera.org/learn/machine-learning)
それではさっそくニューラルネットワークとはどのようなものか、学んでいきましょう。
ニューラルネットワーク(Neural network)
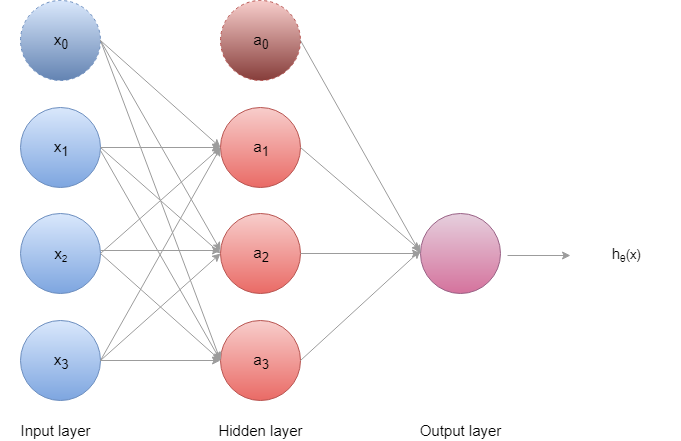
ニューラルネットワークには大きく三つの種類の層(layer)があります。上図の一番左側から入力層(Input layer)、隠れ層(Hidden layer)、出力層(Output layer)となります。
入力層ではまず、入力\(x_1\)~\(x_3\)にバイアスユニット(\(x_0={1,…,1}\))と呼ばれるノードを加え、これらを隠れ層に入力します。隠れ層では各ノードにおいてパラメータθとアクティベーション関数(シグモイド関数やRelu関数)で次のように計算されます。
\(a_1^{(2)}=g(\Theta^{(1)}_{10}x_0+\Theta^{(1)}_{11}x_1+\Theta^{(1)}_{12}x_2+\Theta^{(1)}_{13}x_3)\)
\(a_2^{(2)}=g(\Theta^{(2)}_{10}x_0+\Theta^{(2)}_{11}x_1+\Theta^{(2)}_{12}x_2+\Theta^{(2)}_{13}x_3)\)
\(a_3^{(3)}=g(\Theta^{(3)}_{10}x_0+\Theta^{(3)}_{11}x_1+\Theta^{(3)}_{12}x_2+\Theta^{(3)}_{13}x_3)\)
つまり隠れ層では各ノードでロジスティック回帰を行っているのです。各アクティベーション関数で計算された値は、出力層でも同様にパラメータθとアクティベーション関数によって計算を行い、最終的に”0”か”1”かの分類を行います。
\(h_\Theta(x)\)を見てみると、
\(h_\Theta(x)=g(\Theta^{(2)}_{10}a_0^{(2)}+\Theta^{(2)}_{11}a_1^{(2)}+\Theta^{(2)}_{12}a_2^{(2)}+\Theta^{(2)}_{13}a_3^{(2)})\)
変数がなかなか激しいことになってきました。一旦整理しましょう。
\(x_i\)…入力。この例では3つの特徴変数を持つ。\(x_0\)はバイアスユニットです。
\(a_i^{(j)}\)…アクティベーション関数。上付きと下付きの数字は\(j\)番目の層にある\(i\)番目のノードを意味する。
\(a_2^{(3)}\)であれば、3層目の2つ目のノードということです。
\(\Theta_{ab}^{(j)}\)…\(j\)層にある\(a\)番目のユニットから\(j+1\)層の\(b\)番目のユニットへマッピングするさいの重みづけです。
このとき\(\Theta^{(j)}\)の次元は
(\(j+1\)層のユニットの数) × (\(j\)層+1) 次元の行列で表されます。
さて、以上で頭の中のニューラルネットワークを数式で定義することができました。言い換えると、入力\(x\)をある予測値\(y\)にマッピングする関数を定義してきました。
入力\(x\)をパラメータΘとともにアクティベーション関数に入力し、そしてその出力を出力層のアクティベーション関数へと入力し、最終的に\(h_\Theta (x)\)を計算していく手法をフォーワードプロパゲーションと呼びます。
次回はこのニューラルネットワークを用いて多クラスの分類問題を行っている。つまり、実際にモデルを学習させる方法を学んでいく!
まとめ
・ニューラルネットワークは入力層、隠れ層、出力層を持っており、隠れ層と出力層では各ノードにおいてアクティベーション関数(シグモイド関数等)による計算を行うこで、連続的にロジスティック回帰を行うモデルである
次へ:week4-5 その2 ニューラルネットワークを用いた多クラス分類
- 投稿が見つかりません。


コメント