レコメンダーシステム
Amazonといったインターネットを利用した買い物をするときに検索もしていないのにほしい商品が表示されたりしますよね。
この機能はレコメンダーシステムと呼ばれ、機械学習を利用したとても重要な応用例です。
レコメンダーシステムは私たちユーザがその商品についてどのようなレーティング(評価)をしたか、または過去にユーザどのような商品を購入したかといった情報を利用して、既存のユーザや新たなユーザに商品を紹介したりるすシステムです。
Googleやアマゾンといった今のIT業界にとってかなり重要な技術となるレコメンダーシステムについて説明をしていきます。
さて、まずは例として以下のレーティング結果を見てみましょう。ここでは、たかし、さとし、つよし、きよしの4人に4組のミュージシャンに対して個人的な5段階評価してもらいました。
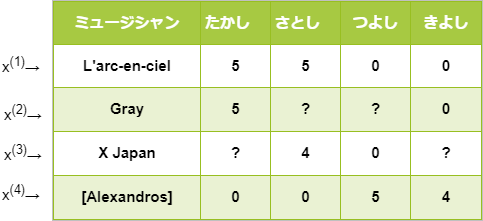
”0”は低評価ではなく、楽曲を聞いたことがないミュージシャンだとします。”?”はこれから機械学習を用いて予測したい評価です。
さて、機械学習を適用するためにいくつかパラメータを定めましょう。
\(x^{(i)}\)…\(i\)番目のミュージシャン
\(r(i,j)\)…\(j\)番目のユーザ、\(i\)番目のミュージシャンの評価の有無。”1”なら評価あり
\(y^{(i,j)}\)…\(j\)番目のユーザによる\(i\)番目のミュージシャンの評価結果
\(\theta^{(j)}\)…\(j\)番目のユーザに定めるパラメータ
\(m^{(j)}\)…\(j\)番目のユーザが評価したミュージシャンの数
\(n_u\)…ユーザの数
\(j\)番目のユーザの、\(i\)番目のミュージシャンの評価を予測するためには以前のブログ(ココ)で勉強した通り仮定関数を用いて、
$$(\theta^{(j)})^T(x^{(i)})$$
を計算しましょう。ユーザの評価値を予測するということは線形回帰モデルを用いた機械学習ですね。
次に、パラメータ\(\theta^{(1)},\theta^{(2)},…,\theta^{(n_u)}\)をそれぞれ計算していきましょう。これに関しても過去に学んでいますよ。(ココ)
$$\min \frac{1}{2} \sum^{n_u}_{j=1} \sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum^{n_u}_{j=1} \sum^n_{k=1}(\theta^{(j)}_k)^2$$
この上記を満たすθを探すために、コスト関数Jに対して最急降下法を使いましょう。
\(k=0\)のとき、
\(\theta^{(j)}_k :=\theta^{(j)}_k-\alpha \sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x^{(i)}_k\)
\(k\neq 0\)のとき、
\(\theta^{(j)}_k :=\theta^{(j)}_k-\alpha (\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x^{(i)}_k+\lambda \theta^{(j)})_k\)
以上によりコスト関数Jを最小化するようなθを求めたら、\(j\)番目のユーザの\(i\)のミュージシャンに対する評価を予測しましょう
$$y^{(i,j)}=(\theta^{(j)})^T(x^{(i)})$$
協調フィルタリング
協調フィルタリングはレコメンダーシステムのアルゴリズムの一つで、アルゴリズムがどのような特徴を使うか、自分自身で学習することができる非常に興味深い性質を持つアルゴリズムです。
好きなミュージシャンのアンケートを取ったとき、全てのユーザが全てのミュージシャンの楽曲を聞いているとは限りません。当然、年代や環境によっては全く聞いたことのないミュージシャンだって多くいることでしょう。
協調フィルタリングは、たとえそのユーザが全く聞いたことのないミュージシャンであっても、学習した\(\theta^{(j)}\)とレーティング\(y^{(i,j)}\)の情報があれば、新たな特徴を予測することができます。
つまり、協調フィルタリングはパラメータ\(\theta\)と特徴\(x\)に対して、\(\theta\)→\(x\)→\(\theta\)→\(x\)→\(\theta\)→\(x\)…と交互に学習していきます。
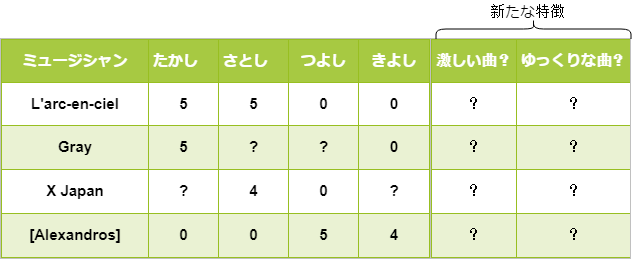
協調フィルタリングは次の手順で行われます。
- \(x^{(1)},x^{(2)},…,x^{(n_m)}\)と\(\theta^{(1)},\theta^{(2)},…,\theta^{(n_u)}\)を小さい値かつランダムに初期化します。
- 最急降下法等を用いてコスト関数\(J(x^{(1)},…,x^{(n_m)},\theta^{(1)},…,\theta^{(n_u)})\)を最小化する\(x\)と\(\theta\)を探します。つまり、全ての\(j=1,…,n_u, i=1,…,n_m\)に対して$$x^{(i)}_k=x^{(i)}_k-\alpha(\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})\theta^{(i)}_k+\lambda x^{(i)}_k)$$ $$\theta^{(i)}_k=\theta^{(i)}_k-\alpha(\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})\theta^{(i)}_k+\lambda x^{(i)}_k)$$を計算し、更新していくことで\(x\)と\(\theta\)を求めていきます。
- ユーザのレーティングが抜けているところに対して$$y^{(i,j)}=(\theta^{(j)})^T(x^{(i)})$$を計算することでレーティングの予測が可能することができます。
平均標準化
さて、ここで全く音楽を聴かない5人目のたけし君がいたとしましょう。
しかしながらたけし君は音楽を聴いたことがないため、最初の四人の評価を参考にたけし君の評価を予測してみましょう。言い換えると、これは4人の評価をもとにたけし君におススメ度を紹介するわけですね。
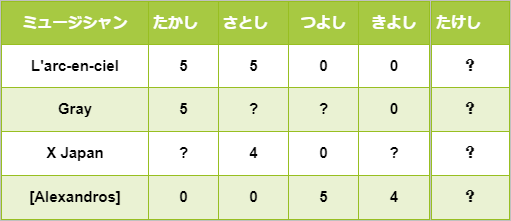
まずは、上記の表をまとめるために行列形式\(Y\)で表現してみましょう。
$$Y=\begin{bmatrix} 5 & 5 & 0 & 0 & ? \\ 5 & ? & ? & 0 & ? \\? & 4 & 0 & ? & ? \\0 & 0 & 5 & 4 & ? \end{bmatrix}$$
次に?を除く各要素の列ごとに平均\(\mu\)を求めて、\(Y\)から引きます。
$$\mu=\begin{bmatrix} 2.5 \\ 2.5 \\2\\2.25 \end{bmatrix}$$
$$Y-\mu=\begin{bmatrix} 2.5 & 2.5 & -2.5 & -2.5 & ? \\ 2.5 & ? & ? & -3.5 & ? \\? & 2 & -2 & ? & ? \\-2.25 & -2.25 & 2.75 & 1.75 & ? \end{bmatrix}$$
\(Y-\mu\)に対して協調フィルタリングを行い、レーティングを予測するとこんな感じになります。
$$X\Theta^T=\begin{bmatrix} (\theta^{(1)})^T(x^{(1)}) & (\theta^{(2)})^T(x^{(1)}) & … & (\theta^{(5)})^T(x^{(1)}) \\ (\theta^{(1)})^T(x^{(2)}) & (\theta^{(2)})^T(x^{(2)}) & … & (\theta^{(5)})^T(x^{(2)}) \\(\theta^{(1)})^T(x^{(3)}) & (\theta^{(2)})^T(x^{(3)}) & … & (\theta^{(5)})^T(x^{(3)}) \\(\theta^{(1)})^T(x^{(4)}) & (\theta^{(2)})^T(x^{(4)}) & … & (\theta^{(5)})^T(x^{(4)}) \end{bmatrix}$$
そして、上の式では平均\(\mu\)だけ引いてしまっているので、レーティングとするためには平均\(\mu\)を足し戻す必要があります。
つまり、\(j\)番目のユーザが\(i\)番目のミュージシャンのレーティングを予測すると
$$(\theta^{(j)})^T(x^{(i)})+\mu_i$$
を計算します。
例えば、先ほどの音楽をあまり聞かないたけし君の場合はなにもレーティングをしていないので\(\theta^{(5)}=[0,0]\)となり、結局、協調フィルタリングの結果は平均値\(\mu\)のみとなります。これまでレーティングをしていた4人の平均がたけし君のレーティングとして表示されるわけです。
まとめ
・レコメンダーシステムはユーザの評価や行動をもとに機械学習によって新しい作品にどのような評価がつくか予測することができる非常に興味深いアルゴリズムである!
・協調フィルタリングによって、ユーザがまだ見ぬミュージシャンや作品に対してどのように評価するかを予測することができる。
私個人的には、協調フィルタリングは非常に興味深いです。機械学習によってお互いのパラメータを学習し合うなんて、ますます人間の手を離れて物事を予測しているような感じがします。
ちょっと数式難しいですが、頑張って理解していきましょう。
- 投稿が見つかりません。


コメント