【初心者流】Courcera 機械学習 Week 8を解く！内容：教師なし学習

さて、今回からは新しい内容に触れていきたいと思います。今まではトレーニングセットには目的変数$y$の値が与えられていましたが、そうではなくただ単にと特徴変数$x$のみ与えられた場合でも機械学習を用いることができます。

例えば、与えられたデータに対して特徴の似たデータ同士をいくつかのグループに分けたいとします。次に説明するクラスタリングの出番です。

教師なし学習　クラスタリング

クラスタリングとは、ラベルのない($y$がない)入力に対して、機械学習によってそのデータのある構造や共通要素、パターン等を探し出して、自動的にグループ分けを行うアルゴリズムであり、教師なし学習の機械学習アルゴリズムの一例です。

このクラスタリングの応用例としては、例えばマーケティングの分野などがあります。

顧客のデータベースに対してセグメンテーションごとにグルーピングをおこなったりするわけです。使い方としては、顧客をいくつかにグルーピングし、それぞれのグループに共通する特徴を見つけ出してマーケティング施策を行うといった使い方です。

その外にも、SNSにおいて同じような使い方をする人たちを調べたり、銀河の形成を理解するといった天文学の分野にもクラスタリングは用いられています。

さて、今回はこのクラスタリングを行うためのアルゴリズムについて説明をしていきたいと思います。

K-meansアルゴリズム

グラスタリングのアルゴリズムでも特に人気の高いK-meansアルゴリズムについて説明を行います。

K-meansアルゴリズムはあるデータをK個のグループに分けるアルゴリズムであり、次のステップを繰り返すことでグループ分けしていきます。

１.　各クラスターの中心点を決める

K個の各クラスターの中心点を決め、各データポイントに対してここで決めたどの中心点に近いかを割り振る。

中心点$\mu _1,\mu_2,…,\mu_K$

下の図では3つの中心点を用いてとりあえずのグループ分けを行います。

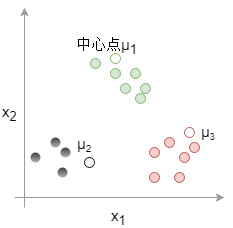
２．中心点の移動

グループ分けされたデータから重心点を求め、各クラスターの中心点をその重心点まで移動させる。

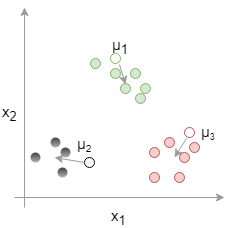
３．繰り返し

中心点が移動したため、ステップ１．を再度行い、各データの割り振りを行う。その後、ステップ2．の中心点の移動を行う。

このステップを重心点が収束するまで何度も繰り返すことで、K個のグループ分けを行います。

K-meansアルゴリズムもまた、通常教師ありの学習と同様にコスト関数があり、それを最小化しようとします。K-meansアルゴリズムはこのコスト関数を最小化することが最終目的となるわけです。

コスト関数は次のようになります。

$$J(c^{(1)},…,c^{(m)},\mu_1,…,\mu_K)=\frac{1}{m}\sum^m_{i=1}||x^{(i)}-\mu_{c^{(i)}}||^2$$

ここで、$c^{(i)}$はクラスターのグループ番号、$\mu_{k}$はクラスター$k$の中心点、$\mu_{c^{(i)}}$はデータの振り分け後に新しく移動する中心点を示します。

つまり、上の式が意味するところは$m$個あるデータのうちの$i$番目のデータ$x^{(i)}$とそのデータの属するグループの重心の位置との間の二乗距離をm個の全データに渡って求めているのです。

このコスト関数Jを最小化しようとパラメータである$c^{(i)}$と$\mu_{i}$を探していきます。

ちなみに、クラスターKの初期の中心点はデータサンプル$x$の中からランダムに選ばれ、またKの数はデータサンプル数mより少ないことが前提となっています。

そしてもう一つ重要なのが、どのようにしてクラスター数Kを選ぶかです。

サンプルデータが上記の図のようにわかりやすく分布していればクラスターの数もなんとなく予測することができるのですが…、データをプロットした見た目からではなかなかクラスターの数を判断することが難しい場合があります。

そのような場合、解決方法としてエルボー法というものがあります。これは、下のグラフのようにクラスター毎にコスト関数の計算を行い、コスト関数Jの変化量が鈍くなったところを選ぶという手法です。

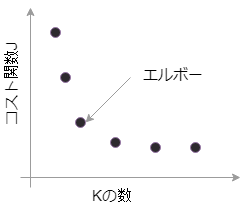
が、、、

実のところ、上のグラフのようにきれいにエルボーが見られることは少なく、通常はもっと変化点が判断しにくいグラフとなってしまいます。

結局のところ、クラスターの数は手動で選ぶ必要があります。グラフからの判断が難しい場合には、データをどのように分けたいのか？グループ分けを行う目的はなんなのか？など、どういう目的でK-meansアルゴリズムを使うのか、という視点から判断する必要があり、ビジネスの側面から考慮する必要があります。

まとめ

・教師なし学習の一つとしてクラスタリングがあり、特に有名なのがK-meansアルゴリズム。

・K-meansアルゴリズムは中心点との距離によってグループ分けを行い、そのグループの重心を新たな中心点として更新し、収束するまで繰り返す。

・クラスターの数Kを求めることが一番難しいかもしれない。(データの分類の仕方や目的を考えてからK-meansアルゴリズムを用いる)

最後に、ランダムイニシャライゼーション(Random initialization)ってなんかかっこいい名前ですよね。

以上！